指数法則再考

---

---

Table of Contents

• 固有名詞
• 指数が自然数のとき
• 指数が整数のとき
• 指数が有理数のとき
• 実数の世界
• 複素数の世界のさわり
• Appendixes
• エピローグ

---

固有名詞

$\square$ 指数表記の各部分の固有名詞

はじめに、もろもろの名称を、あらためて確認しておこう。 $A^\alpha$ と書かれているとき、これを「指数表記」といい、$\alpha$ を「指数」、 $A$ を「底」と呼ぶ。

また、本稿では、次の関係式を「基本指数法則」と呼ぶことにする： \begin{align} A^{\alpha + \beta} &= A^{\alpha}A^{\beta} \;. \label{eq.b0.01} \end{align} そして \begin{align} (AB)^\alpha &= A^\alpha B^\alpha \label{eq.b0.02} \\ (A^\alpha)^\beta &= A^{\alpha\beta} \label{eq.b0.03} \end{align} の２組を指数法則と呼んでいく。

$\square$ 四則演算について

これから、指数や底についての考察を進めていくのであるが、その際には自然数や整数、有理数、実数、複素数が絡み合った四則演算が登場してくるので、それにまつわる大前提をここで述べておきたい。 普段はあまり意識しない事柄であるが、数学的事実（数学的常識？）として暗黙の諒解のうちに適用される、数と四則演算に関する前提である。

• 数どうしの間では、その数的属性（自然数、整数、有理数、実数、複素数）が異なっていても、足し算（加法）と掛け算（乗法）が実践できる。
• 足し算は順序が交換できる（$a + b = b + a$）。
• 掛け算も順序が交換できる（$ab = ba$）。
• 足し算と掛け算においては、結合律、分配律が常に使える（$a(b+c) = ab + ac$）。

加えて、数学を実践するうえでの一般常識として

• 分数の分母は、$0$ であってはならない。
• $1$ は、何回掛けあわせても $1$ である。

がある。

端的に言えば、数の間では躊躇なく四則演算を使って良い、数は $0$ で割ってはいけない、$1 \times 1 \times \cdots \times 1 = 1$ ということである。 これからの記述においては、上記の前提のもとに種々の計算が進められて行っていることを諒解しておいていただけると嬉しい。

---

指数が自然数のとき

$\square$ 生い立ちを想像する

$A$ という「数」を何回か掛け合わせるということの表記方法を（小学校時代（？）まで遡って）振り返ってみよう。 まず、掛けるという行為をあらわす記号として「$\times$」が導入された： \begin{align*} A \times A \times \cdots \times A \;. \end{align*} 少し大人になると（中学生時代か？）、「$\times$」 の代わりに「$\cdot$」を用いたり、それさえも省略する記法も用いられたりする： \begin{align*} A \times A \times \cdots \times A = A \cdot A \cdot \cdots \cdot A = A A \cdots A \;. \end{align*}

「数 $A$ を何回か掛け合わせる」と言うことの表記を簡略化したい。 何回か掛け合わせる、と言うことが焦点になるので、回数を考えることになる。 回数なので、それは勘定可能でなければなるまい。 それゆえ、自然数から始めることが素直である（いきなり $\sqrt{2}$ 回というものを持ち出しても、まずもって想像し難いものだ）。 これが指数表記の生い立ちである、と想像してもいいのではないかと思う（これが歴史的事実なのか、と問われてもわたくしには答えようがないのですが）。

$\square$ $A^n$ という記法を定義する

上記の考察と想像を受けて、$n$ を自然数として、$A$ を $n$ 回掛け合わせることを \begin{align} A^n \equiv \overbrace{A \cdot A \cdot A \cdot \cdots \cdot A}^{n\; \text{個}} \label{eq.n.d.01} \end{align} と記すことにする。 $A^n$ は、日常的には「$A$ の $n$ 乗」と呼ばれる。 さらに、次の２式も定義する： \begin{align} & A^1 \equiv A \label{eq.n.d.02} \;, \\ & A^0 \equiv 1 \label{eq.n.d.03} \;. \end{align} $A^1$ は、$A$ を１回掛けるのだからそれは $A$ である、という自明の事柄の表出である。 $A^0$ については、純粋な取り決めである（この２つの定義の「自然さ」は、指数が整数のときの議論で納得できるのではないかと思う）。

次に、$m$ も自然数であるとして、$A^n$ と $A^m$ を掛けることを考えると \begin{align*} A^n \cdot A^m = \overbrace{A \cdot \cdots \cdot A}^{n\; \text{個}} \cdot \overbrace{A \cdot \cdots \cdot A}^{m\; \text{個}} = A^{n+m} \end{align*} となることは、$A$ を $n + m$ 回掛けたことに他ならないのだから、素直に納得できる。 すなわち、基本指数法則の成立が確認されたのである。

ここまでの議論においては、指数表記の底 $A$ にはなんの制限もない。 すなわち、$A$ がどのような数であっても、指数が自然数の場合には $A^n$ を \eqref{eq.n.d.01} と定義することにより、基本指数法則 \eqref{eq.b0.01} つまり $A^{n+m} = A^nA^m$ が成立することになる。

$\square$ 指数法則の導出

上で述べた $A^n$ の定義を用いて、指数法則を導き出そう。

掛け算が順序交換可能であることから \begin{align*} (AB)^n = \overbrace{AB \cdot AB \cdot AB \cdot \cdots \cdot AB}^{n\; \text{個}} = \overbrace{A \cdot \cdots \cdot A}^{n\; \text{個}} \cdot \overbrace{B \cdot \cdots \cdot B}^{n\; \text{個}} = A^n B^n = B^n A^n \;. \end{align*}

$(A^n)^m$ はどうか。 やはり定義 \eqref{eq.n.d.01} から \begin{align*} (A^n)^m = \overbrace{(A^n) \cdot (A^n) \cdot (A^n) \cdot \cdots \cdot (A^n)}^{m\; \text{個}} \end{align*} であり、基本指数法則を順次使うと、 \begin{align*} \overbrace{(A^n) \cdot (A^n) \cdot (A^n) \cdot \cdots \cdot (A^n)}^{m\; \text{個}} &= A^{n + n} \cdot \overbrace{(A^n) \cdot \cdots \cdot (A^n)}^{m-2\; \text{個}} = A^{n + n + n} \cdot \overbrace{(A^n) \cdot \cdots \cdot (A^n)}^{m-3\; \text{個}} \\ &= A^{\overbrace{n + n + \cdots + n}^{m \; \text{個}}} = A^{mn} \end{align*} となる。ここで $mn = \overbrace{m + m + \cdots + m}^{n\;\text{個}}$ とそのあり様を見直し、かつ再び基本指数法則を使えば \begin{align*} A^{mn} = A^{\overbrace{m + m + \cdots + m}^{n \; \text{個}}} = (A^m) \cdot (A^m) \cdot A^{\overbrace{m + m + \cdots + m}^{n-2 \; \text{個}}} = \overbrace{(A^m) \cdot (A^m) \cdot (A^m) \cdot \cdots \cdot (A^m)}^{n\; \text{個}} = (A^m)^n \end{align*} であるから、結果として（$mn = nm$ であることはもちろんであるからそれも付け加えて） $ (A^n)^m = (A^m)^n = A^{mn} = A^{nm} $ が成り立つことが導き出せる。

$\square$ 付随する法則

$1$ には、「$1$ は何回掛けあわせても $1$ である」という独特の特徴があり、分数どうしの掛け算は分子の掛け算と分母の掛け算を各々独立に計算できるという性質があるから \begin{align*} \left(\frac{1}{A}\right)^n = \overbrace{\frac{1}{A} \cdot \frac{1}{A} \cdot \cdots \cdot \frac{1}{A}}^{n\; \text{個}} = \frac{1^n}{A^n} = \frac{1}{A^n} \end{align*} というように、分子が $1$ の数の $n$ 乗の簡便な表記方法が得られる（もちろんこの場合には $A \neq 0$ という制限がつく）。

$(AB)^n = A^n B^n$ において $B = 1/C$ とすれば（くどいけれど、$C \neq 0$） \begin{align*} \left(\frac{A}{C}\right)^n = \left(A \cdot \frac{1}{C}\right)^n = A^n \cdot \left(\frac{1}{C}\right)^n = A^n \cdot \frac{1}{C^n} = \frac{A^n}{C^n} \;. \end{align*} となる。この結果は、$(AB)^n = A^n B^n$ の特別な場合に他ならない（わざわざ覚えるほどのものではない）。

$\square$ まとめ

指数が自然数の場合についてまとめておこう（$m,\, n$ は自然数）。

• 定義 \begin{align*} & A^n \equiv \overbrace{A \cdot A \cdot A \cdot \cdots \cdot A}^{n\; \text{個}} \\ & A^1 \equiv A \\ & A^0 \equiv 1 \end{align*}
• 基本指数法則 \begin{align*} A^{m+n} = A^mA^n \end{align*}
• 指数法則 \begin{align*} & (AB)^n = A^n B^n = B^n A^n \\ & (A^n)^m = (A^m)^n = A^{mn} = A^{nm} \end{align*}
• 付随的指数法則（覚えるまでもないが、覚えておいても損はない） \begin{align*} & \left(\frac{1}{A}\right)^n = \frac{1}{A^n} \\ & \left(\frac{A}{B}\right)^n = \frac{A^n}{B^n} \end{align*}

ここまでで、底 $A、B$ には、分母に現れたときには $0$ でないと言う以外には、いまのところなんの制限もなかった。 それゆえ、指数が自然数の場合は、指数法則は（分母は $0$ でないと言う制限以外には）底の数的属性によらず問題なく成立する、という結果が得られたのである。

---

指数が整数のとき

$\square$ $A^{-n}$ を定義する

指数が整数のときでも、基本指数法則 $A^{\alpha+\beta} = A^\alpha A^\beta$ \eqref{eq.b0.01} が成り立つようにしたい。 $n,\, m$ が自然数のときに成立していることは、上の節で見た。 したがって、$-n,\, -m$ のときにも成立するようにすれば、整数全体でも成立することになる。 そのためには、$A^{-n}$ をどう取り決めれば良いだろうか？

指数が整数の時にも基本指数法則が成り立つとすると、形式的には \begin{align*} A^{n + (-n)} = A^n A^{-n} \end{align*} ということになる。 一方で \begin{align*} \quad A^{n + (-n)} = A^0 = 1 \end{align*} でもあるから、あわせると \begin{align*} A^n A^{-n} = 1 \quad \Longrightarrow\; A^{-n} = \frac{1}{A^n} \end{align*} という計算結果が得られる。 これを逆手にとって \begin{align} A^{-n} \equiv \frac{1}{A^n} \label{eq.i.d.01} \end{align} と定義することにしてしまう。 いわゆる「定義化」、つまり辻褄の合うようにあたらしいものを決める、という手段の採用である。 この定義からくる $A$ についての制限は、$A \neq 0$ である。 指数を整数にまで拡張するためには、底は $0$ ではない、という制限が付加される。 それを踏まえて、この定義の「自然さ」について少し考えてみよう。 $n$ が自然数のときの $A$ の $n$ 乗は \begin{align*} A^1 \equiv A \;, \quad A^{n+1} = A^n A \end{align*} というように帰納的な定義としてあらわすことができる。 これを $A^3$ から始めて $1$ まで下っていくと \begin{align*} & A^3 = A^2 A \\ & A^2 = A^1 A \\ & A^1 = A^0 A = A \end{align*} であるから、指数を $-n$ にまで広げてみると、定義 $A^0 \equiv 1$ \eqref{eq.n.d.03} を利用すれば \begin{alignat*}{2} & A^0 = A^{-1} A & &\quad\Longrightarrow\; A^{-1} = \frac{1}{A} \\ & A^{-1} = A^{-2} A & &\quad\Longrightarrow\; A^{-2} = \frac{1}{A^2} \\ & A^{-2} = A^{-3} A & &\quad\Longrightarrow\; A^{-3} = \frac{1}{A^3} \\ & \cdots\cdots & &\quad\cdots\cdots \\ & A^{-n+1} = A^{-n} A & &\quad\Longrightarrow\; A^{-n} = \frac{1}{A^n} \\ \end{alignat*} であって欲しいという「自然」な願望がでてくる。 この願望が定義 $A^{-n} \equiv \dfrac{1}{A^n}$ \eqref{eq.i.d.01} の自然さを支えており、なかんづく $A^1 \equiv A$ \eqref{eq.n.d.02}、$A^0 \equiv 1$ \eqref{eq.n.d.03} の定義の正当性を支えているのである。

$\square$ 基本指数法則を確認する

$A^{-n}$ の定義 \eqref{eq.i.d.01} を素直に用いれば \begin{align*} A^{-n}A^{-m} = \frac{1}{A^n} \cdot \frac{1}{A^m} = \frac{1}{A^{n+m}} = A^{-(n + m)} = A^{(-n) + (-m)} \end{align*} となって、指数がともに負の整数の場合でも基本指数法則が成り立っていることがわかる。

正負の指数が混じり合っている場合をみると \begin{align*} A^nA^{-m} = \frac{A^n}{A^m} \end{align*} であり、ここで分子と分母で約分を実行してしまえば \begin{align*} \frac{A^n}{A^m} = \begin{cases} n \gt m \;\Longrightarrow\; A^{n-m} \\ n = m \;\Longrightarrow\; 1 \\ n \lt m \;\Longrightarrow\; \dfrac{1}{A^{m-n}} = A^{n-m} \end{cases} \end{align*} となり、やはり基本指数法則が成り立っている。

以上から、指数が整数のときでも、基本指数法則は問題なく成立することがわかった。

$\square$ 指数法則を確認する

指数法則 \eqref{eq.b0.02} を確認してみよう。 $(AB)^{-n} = \dfrac{1}{(AB)^n}$ であるから指数が自然数の場合の法則が利用でき、 \begin{align*} (AB)^{-n} = \frac{1}{(AB)^n} = \frac{1}{A^n B^n} = \frac{1}{A^n} \cdot \frac{1}{B^n} = A^{-n}B^{-n} \end{align*} となって、$AB \neq 0$ であるかぎり、指数が負の整数であっても、この指数法則が成り立つことがわかった。 ちなみに、$AB \neq 0$ は、$A$ と $B$ はともに $0$ ではない、ということであり、複素数においてもこの事実は成立するのである。

つぎに指数法則 \eqref{eq.b0.03} をみてみよう。 まず指数の片方が負である場合を見てみると \begin{align*} (A^{-n})^m = \left(\frac{1}{A^n}\right)^m = \frac{1}{A^{nm}} = A^{-nm} \end{align*} であり、 \begin{align*} (A^n)^{-m} = \frac{1}{(A^n)^m} = \frac{1}{A^{nm}} = A^{-nm} \end{align*} となるから、 \begin{align*} (A^{-n})^m = A^{-nm} = A^{-mn} = (A^{m})^{-n} \end{align*} である。 ２つの指数が共に負である場合は、ここまでの結果を用いて \begin{align*} &(A^{-n})^{-m} = \frac{1}{(A^{-n})^m} = \frac{1}{A^{-nm}} = A^{nm} \;, \quad (A^{-m})^{-n} = \frac{1}{(A^{-m})^n} = \frac{1}{A^{-nm}} = A^{nm} \\ &\therefore\; (A^{-n})^{-m} = A^{nm} = A^{mn} = (A^{-m})^{-n} \;. \end{align*}

上記の結果から、整数全体でも指数法則が成立することが見て取れた。

$\square$ 付随する法則

この結果から、次の関係が存在することもわかる： \begin{align*} \left(\frac{1}{A}\right)^{-n} = \frac{1}{\left(\frac{1}{A}\right)^n} = \frac{1}{A^{-n}} = A^n \;. \end{align*} さらにこの結果を利用して \begin{align*} \left(\frac{A}{B}\right)^{-n} = \left(A \cdot \frac{1}{B}\right)^{-n} = A^{-n} \cdot \left(\frac{1}{B}\right)^{-n} = \frac{1}{A^n} \cdot B^n = \frac{B^n}{A^n} = \left(\frac{B}{A}\right)^n \;. \end{align*}

$\square$ まとめ

ここまで自然数 $m,\, n$ において $-m$ や $-n$ の場合を考察してきたので、それらを整数 $k,\, l$ に繰り込むことができる。 指数が整数にまで拡張された場合についてまとめよう。

• 条件

  底 $A,\, B$ はともに $0$ ではない。

• 定義 \begin{align*} & A^n \equiv \overbrace{A \cdot A \cdot A \cdot \cdots \cdot A}^{n\; \text{個}} \\ & A^1 \equiv A \\ & A^0 \equiv 1 \\ & A^{-n} \equiv \frac{1}{A^n} \end{align*}
• 基本指数法則 \begin{align*} A^{k+l} = A^kA^l \end{align*}
• 指数法則 \begin{align*} & (AB)^k = A^k B^k = B^k A^k \\ & (A^k)^l = (A^l)^k = A^{kl} = A^{lk} \end{align*}
• 付随的指数法則（理解のために、自然数の場合の記述を対比しておく） \begin{alignat*}{2} & A^{k-l} = \frac{A^k}{A^l} \qquad & &\left( A^{n-m} = \frac{A^n}{A^m} \right) \\ & \left(\frac{1}{A}\right)^k = \frac{1}{A^k} \iff \left(\frac{1}{A}\right)^{-k} = A^k \qquad & &\left( \left(\frac{1}{A}\right)^n = \frac{1}{A^n} \iff \left(\frac{1}{A}\right)^{-n} = A^n \right) \\ & \left(\frac{A}{B}\right)^k = \frac{A^k}{B^k} \iff \left(\frac{A}{B}\right)^{-k} = \left(\frac{B}{A}\right)^k = \frac{B^k}{A^k} \qquad & &\left( \left(\frac{A}{B}\right)^n = \frac{A^n}{B^n} \iff \left(\frac{A}{B}\right)^{-n} = \left(\frac{B}{A}\right)^n = \frac{B^n}{A^n} \right) \end{alignat*}

---

指数が有理数のとき

$\square$ $n$ 乗根

指数が有理数である数とはどのようなものなのかを、$n$ 次方程式 $x^n = A$ （$n$ は自然数）を考えることから始めてみよう。 この $n$ 次方程式の根となる数 $x$ には「$A$ の $n$ 乗根」という名前がついている（$2$乗根には平方根、$3$乗根には立方根という慣用名もある）。 例えば $(-2)^2 = 4$ であり、また、$2^2 = 4$ でもあるから、 $-2$ と $2$ はともに $4$ の $2$ 乗根である。 $(-3)^3 = -27$ であるから、$-3$ は $-27$ の $3$ 乗根。 純虚数 $i$ についても、$i^3 = -i$ であるから、$i$ は $-i$ の $3$ 乗根である。

では、$n$ 乗根はいくつあるのだろうか？ ここで、「代数学の基本定理」の簡略版 \begin{align*} \text{$x^n = A$ を満たす $x$ は、複素数の範囲で（つまり、$x$ も $A$ も複素数の範囲で）、$n$ 個存在する} \end{align*} を事実として認め、援用しよう（証明は本稿の範囲を遥かに超える）。 この事実は、$A$ の $n$ 乗根は $n$ 個存在する、とも言い換えられる（堅苦しいことを言えば、「重複を含めて」$n$ 個ということになる）。 例えば、$x^3 = 1$ という方程式には、複素数の範囲まで考慮すると \begin{align*} x^3 = 1 \iff x = \begin{cases} 1 \\ \left(-1 + \sqrt{3}i\right)/2 \\ \left(-1 - \sqrt{3}i\right)/2 \end{cases} \end{align*} という３つの根があることは著名な事実である（いきなり $\sqrt{3}$ を用いてしまったが、この記号については後述する）。

上記を踏まえて、$x^n = A$ の根を $\set{A^\frac{1}{n}}$ のように集合として表記することにする。 すなわち、集合 $\set{A^\frac{1}{n}}$ を、自分自身を $n$ 回掛け合わせると $A$ になる数を要素とする集合である、というように決めるのである。 言い換えれば、$\set{A^\frac{1}{n}}$ は、$A$ の $n$ 乗根の集合、ということになる。 したがって、次の事実が成立する： \begin{align*} p \in \set{A^\frac{1}{n}} \quad\iff\quad p^n = A \;. \end{align*} そして複素数の範囲までを対象とすると、$\set{A^\frac{1}{n}}$ には $n$ 個の要素が存在するのである。

$\square$ $A^\frac{m}{n}$ の解釈

$A^\frac{m}{n}$ （$n,\, m$ は自然数）はどう扱えば良いだろうか。 $A^\frac{m}{n}$ には、形式的には \begin{align} A^\frac{m}{n} = \left(A^\frac{1}{n}\right)^m \quad\text{または}\quad A^\frac{m}{n} = \left(A^m\right)^\frac{1}{n} \label{eq.r.00} \end{align} という２通りの計算手順の解釈が存在する。 この解釈の相違によって計算結果が異なるということはあるのか、ということを考えてみる。

$n$ 乗根どうしの関係

まず $A$ の $n$ 乗根の集合の要素を $ \set{A^\frac{1}{n}} = \set{p_1, p_2, \ldots, p_n} $ と列挙するようにすれば、 \begin{align*} p_j^n = A \quad (j = 1, \ldots, n) \end{align*} である。 また $A^m$ の $n$ 乗根の集合の要素を $ \set{\left(A^m\right)^\frac{1}{n}} = \set{q_1, q_2, \ldots, q_n} $ と列挙すれば \begin{align*} q_k^n = A^m \quad (k = 1, \ldots, n) \end{align*} となる。 したがって、 \begin{align*} q_k^n = (p_j^n)^m \end{align*} であり、$n,\,m$ ともに自然数であるから、自然数を指数とする場合の指数法則が利用できて \begin{align} q_k^n = (p_j^n)^m \iff q_k^n = p_j^{mn} \iff \left(\frac{p_j^{mn}}{q_k^n}\right) = 1 \iff \left(\frac{p_j^m}{q_k}\right)^n = 1 \iff \frac{p_j^m}{q_k} \in \set{1^\frac{1}{n}} \label{eq.r.01} \end{align} という結果が得られる。 ここまでの計算では、$j$ と $k$ の選び方は任意である。 つまりどのように $p_j$ と $q_k$ を選んでもこの結果は成立するのである。 そしてさらに、この $p_j^m/q_k$ は、$1$ の $n$ 乗根全てをカバーしているのである（これはおそらく証明が必要だろう）。 ううむ、恐ろしい。 言葉で書いてみると \begin{align*} \frac{\left(\text{$A$ の $n$ 乗根のどれか}\right)^m}{\left(\text{$A^m$ の $n$ 乗根のどれか}\right)} = \left(\text{$1$ の $n$ 乗根のどれか}\right) \;. \end{align*}

実数という制限をつける

再び $ \set{A^\frac{1}{n}} = \set{p_1, p_2, \ldots, p_n},\; \set{\left(A^m\right)^\frac{1}{n}} = \set{q_1, q_2, \ldots, q_n} $ とあらわした $n$ 乗根の集合に戻ろう。 これらの要素の間には \eqref{eq.r.01} で見たように $ (p_j^m/q_k)^n = 1 \iff p_j^m/q_k \in \set{1^\frac{1}{n}} $ という関係が存在していた。 しかしながら、この $p_j$ と $q_k$ の組み合わせには $n \times n$ 通りあって、色々とややこしい。 そこで、「$A$ は実数である」という特別な条件を課して、問題を縮小してみることにする。 記法に条件を繰り込ませるために、実数であるという事柄を $R$ というサフイックスであらわそう。 すなわち、$A_R$ とあれば、$A_R$ は実数であると諒解するのである。

$n$ 乗根にまつわる今までの議論では、$A$ はどんな数でも良かった。 したがって、$A_R$ の $n$ 乗根についても同じ理路を用いることができる。 その上で、実数 $A_R$ と限定することにより、$n$ 乗根の集合にはいくつかの特徴があらわれてくる。

$p$ を $A_R$ の $n$ 乗根、つまり、$p^n = A_R$ であるとしよう。 このとき、$n$ の偶奇（even/odd）に関連して次の事実が存在する： \begin{align*} & n: odd \Rightarrow A_R \;\text{の $n$ 乗根のうち、実数のものが一つのみ存在する} \\ & n: even \Rightarrow \begin{cases} A_R \gt 0 \;\text{の時には $n$ 乗根で実数のものが $2$ 個存在する（絶対値は同じで符号がことなる）} \\ A_R \lt 0 \;\text{の時には $n$ 乗実数根は存在しない} \end{cases} \end{align*} （上記の事実については、appendix3 で説明を記した）

$n$ が奇数（odd）の時の実数の $n$ 乗根を $p_R$、$n$ が偶数の時の実数である２つの $n$ 乗根を $p_{R+},\, -p_{R+}\, (p_{R+} \gt 0)$ と書くことにすると、$A_R$ の $n$ 乗根の集合は \begin{align*} & n: odd \Rightarrow \set{A_R^\frac{1}{n}} = \set{p_R, p_2, p_3, \ldots, p_n} \\ & n: even \Rightarrow \begin{cases} A_R \gt 0 \Rightarrow \set{A_R^\frac{1}{n}} = \set{p_{R+}, -p_{R+}, p_3, p_4, \ldots, p_n} \\ A_R \lt 0 \Rightarrow \set{A_R^\frac{1}{n}} = \set{p_1, p_2, \ldots, p_n} \;\text{（実数である要素はない）} \end{cases} \end{align*} と表記できよう。 そして、$A_R$ が実数であるから当然 $A_R^m$ も実数であるので $q^n = (A_R)^m$ として、上と同様に $q_R,\, q_{R+},\, -q_{R+}$ を定めれば \begin{align*} & n: odd \Rightarrow \set{\left(A_R^m\right)^\frac{1}{n}} = \set{q_R, q_2, q_3, \ldots, q_n} \\ & n: even \Rightarrow \begin{cases} A_R^m \gt 0 \Rightarrow \set{\left(A_R^m\right)^\frac{1}{n}} = \set{q_{R+}, -q_{R+}, q_3, q_4, \ldots, q_n} \\ A_R^m \lt 0 \Rightarrow \set{\left(A_R^m\right)^\frac{1}{n}} = \set{q_1, q_2, \ldots, q_n} \;\text{（実数である要素はない）} \end{cases} \end{align*} となる。 ここで、 \eqref{eq.r.01} でみた $(p_j^m/q_k)^n = 1$ という関係を利用しよう。 $j$ と $k$ の選び方は任意だったことを思い出して、実数根どうしの組み合わせをみてみる。

• $n: odd$ のとき

  $\displaystyle{ \left(\frac{p_R^m}{q_R}\right)^n = 1 \iff p_R^m = q_R }$ （これが帰結されることについては appendix4 参照）。

• $n: even,\, A_R \gt 0$ のとき

  $A_R \gt 0$ であるから当然 $A_R^m \gt 0$ である。したがって実数根どうしの組み合わせは \begin{align*} \frac{p_{R+}^m}{q_{R+}}, \quad \frac{p_{R+}^m}{-q_{R+}}, \quad \frac{-p_{R+}^m}{q_{R+}}, \quad \frac{-p_{R+}^m}{-q_{R+}} \end{align*} の４通りあるけれども、 \begin{align*} \frac{-p_{R+}^m}{-q_{R+}} = \frac{p_{R+}^m}{q_{R+}} \;, \quad \frac{p_{R+}^m}{-q_{R+}} = \frac{-p_{R+}^m}{q_{R+}} = - \frac{p_{R+}^m}{q_{R+}} \end{align*} なので実質は２通りである。 そして $p_{R+} \gt 0,\, q_{R+} \gt 0,\, n: even$ であること、さらに $n$ は自然数であるから指数法則が適用できることに留意すると \begin{align*} & \left(\frac{p_{R+}^m}{q_{R+}}\right)^n = 1 \iff p_{R+}^m = q_{R+} \;, \\ & \left(-\frac{p_{R+}^m}{q_{R+}}\right)^n = 1 \iff (-1)^n\left(\frac{p_{R+}^m}{q_{R+}}\right)^n = 1 \iff \left(\frac{p_{R+}^m}{q_{R+}}\right)^n = 1 \iff p_{R+}^m = q_{R+} \end{align*} となり、どの組み合わせの場合においても、$p_{R+}^m = q_{R+}$ になる（この結果が帰結されることについても appendix4 参照）。

• $n: even,\, A_R \lt 0$ のとき

  $A_R$ の $n$ 乗根で実数であるものが存在しないので、考察の対象外にする （$(A_R)^m$ の $n$ 乗根には $m$ が偶数であれば実数であるものが存在するけれど、そもそもの $A_R$ の $n$ 乗根が存在しないので考えても意味がない）。

$A_R^\frac{m}{n}$ の存在条件

さていよいよ $A^\frac{m}{n}$ の解釈である。 ここまで見てきたように、底を実数 $A_R$ に限定し、かつ、$n$ 乗根を実数であるものだけに限定して、さらに $p_R,\,q_R,\, p_{R+},\, q_{R+}$ の定義を踏襲することにして \begin{align*} n: odd &\;\Rightarrow\; A_R^\frac{1}{n} \equiv p_R \;, \\ n: even &\;\Rightarrow\; \begin{cases} A_R \gt 0 \;\Rightarrow\; A_R^\frac{1}{n} \equiv p_{R+} \;, \\ A_R \lt 0 \;\Rightarrow\; A_R^\frac{1}{n} \text{は存在しない} \end{cases} \end{align*} というように $A_R^\frac{1}{n}$ を定義することにする。 $n$ が偶数で $A_R \gt 0$ のとき、$A_R^\frac{1}{n}$ には $-p_{R+}$ という候補も存在するけれども、正の実数根の方をあらわすというように取り決めるのである （それゆえ $-A_R^\frac{1}{n} = -p_{R+}$ という取り決めにもなる）。 この定義のもとで、$p_R^m = q_R$ や $p_{R+}^m = q_{R+}$ という関係を適用すれば \begin{align} \left. \begin{aligned} n: odd &\;\Rightarrow\; \left(p_R^m = q_R \iff \left(A_R^\frac{1}{n}\right)^m = \left(A_R^m\right)^\frac{1}{n}\right) \\ n: even,\, A_R \gt 0 &\;\Rightarrow\; \left(p_{R+}^m = q_{R+} \iff \left(A_{R}^\frac{1}{n}\right)^m = \left(A_R^m\right)^\frac{1}{n}\right) \end{aligned} \label{eq.r.02} \right\} \end{align} が得られる。 したがって、$n$ が奇数でも偶数でも、$A_R \gt 0$ のときには、すべての自然数 $n,\, m$ において $\displaystyle{ \left(A_{R}^\frac{1}{n}\right)^m = \left(A_R^m\right)^\frac{1}{n} }$ となる。 $A_R \lt 0$ のときには、$n$ が奇数のときに限って $\displaystyle{ \left(A_{R}^\frac{1}{n}\right)^m = \left(A_R^m\right)^\frac{1}{n} }$ となる（$m$ は任意の自然数でかまわない）。 $A_R$ に焦点をあてて場合分けを記述しなおせば（$A_R$ の場合分けを記号に含める、すなわち、$A_{R+}\;(\gt 0),\, A_{R-}\;(\lt 0)$ という表記をもちいる）、 \begin{align} \left. \begin{aligned} \text{$n,\, m$ は任意の自然数で} &\;\Rightarrow\; \left(A_{R+}^\frac{1}{n}\right)^m = \left(A_{R+}^m\right)^\frac{1}{n} \\ \text{$n$ が奇数、$m$ は任意の自然数で} &\;\Rightarrow\; \left(A_{R-}^\frac{1}{n}\right)^m = \left(A_{R-}^m\right)^\frac{1}{n} \end{aligned} \label{eq.r.03} \right\} \end{align} である。 この \eqref{eq.r.02} または \eqref{eq.r.03} を（この２つは同値であることは言うまでもない）「$A_R^\frac{m}{n}$ の存在条件」と呼ぶことにしよう。

この節の始めで述べた「計算手順が異なっても結果は同じかという疑問 \eqref{eq.r.00}」は、

• すべての数を対象としていた底 $A$ を $A_R$ というように実数に限定する（問題の縮小化）
• $A_R^\frac{1}{n}$ を、$n$ 乗根のうちで実数であるものとし、かつ $n$ が偶数のときには正の方を採用する、と定義する

という方針をとることによって、今まとめた $A_R^\frac{m}{n}$ の存在条件 \eqref{eq.r.02} または \eqref{eq.r.03} のもとで、計算手順が異なっても結果は同じである、という結論が導かれるのである。 結果が同じとなるので、この場合には \begin{align*} & A_{R+}^\frac{m}{n} = \left(A_{R+}^\frac{1}{n}\right)^m = \left(A_{R+}^m\right)^\frac{1}{n} \quad\text{（$n,\, m$ は任意の自然数）} \\ & A_{R-}^\frac{m}{n} = \left(A_{R-}^\frac{1}{n}\right)^m = \left(A_{R-}^m\right)^\frac{1}{n} \quad\text{（$n$ は奇数、$m$ は任意の自然数）} \end{align*} と書くことが認められよう。

$\square$ 基本指数法則の導出

ここまでの準備のもとで、指数が有理数の場合でも基本指数法則が満たされるかどうかをみてみよう（以下 $m,\, n,\, j,\, k$ は自然数）。

$A_{R+}$ においては、すべての自然数 $n,\, m$ において $A_{R+}^\frac{m}{n} = (A_{R+}^m)^\frac{1}{n} = \left(A_{R+}^\frac{1}{n}\right)^m$ が成り立つから \begin{alignat*}{2} A_{R+}^{\frac{m}{n} + \frac{j}{k}} = A_{R+}^{\frac{mk + jn}{nk}} &= \left(A_{R+}^{\frac{1}{nk}}\right)^{mk + jn} & &\quad\text{（$mk,\, jn$ は整数となるので基本指数法則が使える）} \\ &= \left(A_{R+}^{\frac{1}{nk}}\right)^{mk}\left(A_{R+}^{\frac{1}{nk}}\right)^{jn} & & \\ &= A_{R+}^{\frac{mk}{nk}}A_{R+}^{\frac{jn}{nk}} & &\quad\text{（指数部分の約分にて）} \\ &= A_{R+}^{\frac{m}{n}}A_{R+}^{\frac{j}{k}} \;. & & \end{alignat*}

$A_{R-}$ においては、$n$ が奇数の時にのみ $A_{R-}^\frac{m}{n} = (A_{R-}^m)^\frac{1}{n} = \left(A_{R-}^\frac{1}{n}\right)^m$ が成り立つのであった。 したがって $A_{R-}^\frac{j}{k}$ が存在するためには $k$ も奇数でなければならない。 その上で \begin{alignat*}{2} A_{R-}^{\frac{m}{n} + \frac{j}{k}} = A_{R-}^\frac{mk + jn}{nk} &= \left(A_{R-}^\frac{1}{nk}\right)^{mk + jn} & &\quad\text{（$n,\, k$ ともに奇数だから $nk$ も奇数）} \\ &= \left(A_{R-}^\frac{1}{nk}\right)^{mk}\left(A_{R-}^\frac{1}{nk}\right)^{jn} & &\quad\text{（$nk$ は奇数だから、$mk,\, jn$ が肩から降りる）} \\ &= A_{R-}^\frac{mk}{nk} A_{R-}^\frac{jn}{nk} & & \\ &= A_{R-}^\frac{m}{n} A_{R-}^\frac{j}{k} \;. & & \end{alignat*}

結果として

• 任意の自然数 $m,\, n,\, j,\, k$ で $\displaystyle{ \quad A_{R+}^{\frac{m}{n} + \frac{j}{k}} = A_{R+}^\frac{m}{n} A_{R+}^\frac{j}{k} }$
• $n,\, k$ が奇数（つまり分母が奇数）、$m,\, j$ は任意の自然数で $\displaystyle{ \quad A_{R-}^{\frac{m}{n} + \frac{j}{k}} = A_{R-}^\frac{m}{n} A_{R-}^\frac{j}{k} }$

となり、基本指数法則が満たされていることが示せたのである。

$\square$ 指数法則の導出

指数法則 \eqref{eq.b0.02} を導く

指数表記の底がすべて正の実数の場合から考える。 $C = A_{R+}^\frac{m}{n},\, D = B_{R+}^\frac{m}{n}$ とすれば \begin{align*} & C = A_{R+}^\frac{m}{n} = \left(A_{R+}^m\right)^\frac{1}{n} \iff C^n = A_{R+}^m \;, \\ & D = B_{R+}^\frac{m}{n} = \left(B_{R+}^m\right)^\frac{1}{n} \iff D^n = B_{R+}^m \end{align*} となるから \begin{align*} C^n D^n = A_{R+}^m B_{R+}^m &\iff (CD)^n = (A_{R+}B_{R+})^m \\ &\iff CD = \left((A_{R+}B_{R+})^m\right)^\frac{1}{n} = (A_{R+}B_{R+})^\frac{m}{n} \\ &\iff A_{R+}^\frac{m}{n} B_{R+}^\frac{m}{n} = (A_{R+}B_{R+})^\frac{m}{n} \;. \end{align*} これより、 $(A_{R+}B_{R+})^\frac{m}{n} = A_{R+}^\frac{m}{n} B_{R+}^\frac{m}{n}$ が得られた。

指数表記の底がすべて負の実数の場合では、$n$ は奇数でなければならない。 その前提のもとで $C = A_{R-}^\frac{m}{n},\, D = B_{R-}^\frac{m}{n}$ と置いて上と同様な計算をすればよい。 結果として、 $(A_{R-}B_{R-})^\frac{m}{n} = A_{R-}^\frac{m}{n} B_{R-}^{\frac{m}{n}}$ が得られる。

指数表記の底が正負混在しているとき、すなわち $(A_{R+}B_{R-})^\frac{m}{n}$ という場合を考えてみよう。 $A_{R+}B_{R-} \lt 0$ はあきらからであるから、$n$ が奇数でないと $(A_{R+}B_{R-})^\frac{m}{n}$ は存在しない。 また、$n$ が奇数ならば $C = A_{R+}^\frac{m}{n},\, D = B_{R-}^\frac{m}{n}$ は両方とも存在するので、まったく同じ論法によって $A_{R+}^{\frac{m}{n}}B_{R-}^\frac{m}{n} = (A_{R+}B_{R-})^\frac{m}{n}$ となっていることがわかる。

指数法則 \eqref{eq.b0.03} を導く

指数表記の底がすべて正の実数の場合、 $F = A_{R+}^\frac{mj}{nk}$ とすると \begin{align*} F = A_{R+}^\frac{mj}{nk} = \left(A_{R+}^{mj}\right)^\frac{1}{nk} \iff F^{nk} = A_{R+}^{mj} \;. \end{align*} また $G = \left(A_{R+}^\frac{m}{n}\right)^\frac{j}{k}$ とすれば、ここでも \begin{align*} G = \left(A_{R+}^\frac{m}{n}\right)^\frac{j}{k} = \left(\left(A_{R+}^\frac{m}{n}\right)^j\right)^\frac{1}{k} \iff G^k = \left(A_{R+}^\frac{m}{n}\right)^j = \left(A_{R+}^{mj}\right)^\frac{1}{n} \iff G^{nk} = A_{R+}^{mj} \end{align*} とあらわせる。したがって \begin{align*} F^{nk} = G^{nk} \iff \frac{F^{nk}}{G^{nk}} = \left(\frac{F}{G}\right)^{nk} = 1 \end{align*} となり、また、$F \gt 0,\, G \gt 0$ であるから（appendix4 でみたように） \begin{align*} \left(\frac{F}{G}\right)^{nk} = 1 \iff \frac{F}{G} = 1 \iff F = G \iff A_{R+}^\frac{mj}{nk} = \left(A_{R+}^\frac{m}{n}\right)^\frac{j}{k} \;. \end{align*}

指数表記の底が負の実数の場合は、最後のロジックが異なる。$n,\, k$ を奇数という前提で $F = A_{R-}^\frac{mj}{nk},\, G = \left(A_{R-}^\frac{m}{n}\right)^\frac{j}{k}$ とおいて \begin{align*} F^{nk} = G^{nk} \iff \frac{F^{nk}}{G^{nk}} = \left(\frac{F}{G}\right)^{nk} = 1 \end{align*} となるところまでは、底が正数の場合とかわらない。 違いは、$nk$ は奇数であるから、実数の範囲では奇数回かけあわせて $1$ になる数は $1$ しか存在しない（appendix4 でみたように）、という結果を使うところにある。 それゆえ \begin{align*} \frac{F}{G} = 1 \iff F = G \iff A_{R-}^\frac{mj}{nk} = \left(A_{R-}^\frac{m}{n}\right)^\frac{j}{k} \;. \end{align*}

$\square$ 付随する指数法則

• $\displaystyle{\left(\frac{1}{A_{R+}}\right)^\frac{m}{n} = \dfrac{1}{A_{R+}^\frac{m}{n}}}$ （$n,\, m$ は任意の自然数）

  まず最初に $\displaystyle{ J = \left(\frac{1}{A_{R+}}\right)^\frac{m}{n} }$ を考えると \begin{align*} J^n = \left(\frac{1}{A_{R+}}\right)^m = \frac{1^m}{A_{R+}^m} = \frac{1}{A_{R+}^m} \;. \end{align*} つぎに $\displaystyle{ K = \frac{1}{A_{R+}^\frac{m}{n}} }$ を考えると \begin{align*} K^n = \left(\frac{1}{A_{R+}^\frac{m}{n}}\right)^n = \frac{1^n}{\left(A_{R+}^\frac{m}{n}\right)^n} = \frac{1}{A_{R+}^m} \;. \end{align*} したがって \begin{align*} J^n = K^n \iff \frac{J^n}{K^n} = 1 \iff \left(\frac{J}{K}\right)^n = 1 \end{align*} であり、$J \gt 0,\, K \gt 0$ であるから \begin{align*} \left(\frac{J}{K}\right)^n = 1 \iff \frac{J}{K} = 1 \iff J = K \iff \left(\frac{1}{A_{R+}}\right)^\frac{m}{n} = \frac{1}{A_{R+}^\frac{m}{n}} \;. \end{align*}

  
  
• $\displaystyle{\left(\frac{1}{A_{R-}}\right)^\frac{m}{n} = \dfrac{1}{A_{R-}^\frac{m}{n}}}$ （$n$ は奇数）

  $\displaystyle{ J = \left(\frac{1}{A_{R-}}\right)^\frac{m}{n} ,\, K = \frac{1}{A_{R+}^\frac{m}{n}} }$ とすれば、上と同様にして \begin{align*} J^n = K^n \iff \left(\frac{J}{K}\right)^n = 1 \end{align*} がもとまる。 $n$ は奇数であるから奇数回かけあわせて $1$ になる実数は $1$ しかない（appendix4 でみたように）。 それゆえ \begin{align*} \left(\frac{J}{K}\right)^n = 1 \iff \frac{J}{K} = 1 \iff J = K \iff \left(\frac{1}{A_{R-}}\right)^\frac{m}{n} = \frac{1}{A_{R-}^\frac{m}{n}} \;. \end{align*}

  
  
• $\displaystyle{ \left(\frac{A_{R+}}{B_{R+}}\right)^\frac{m}{n} = \frac{A_{R+}^\frac{m}{n}}{B_{R+}^\frac{m}{n}} }$ （$n,\, m$ は任意の自然数）

  $(A_{R+}C_{R+})^\frac{m}{n} = A_{R+}^{\frac{m}{n}}C_{R+}^\frac{m}{n}$ は成立していた。 よって、 $\displaystyle{ C_{R+} = \frac{1}{B_{R+}} }$ とすれば、 $\displaystyle{ \left(\frac{A_{R+}}{B_{R+}}\right)^\frac{m}{n} = \frac{A_{R+}^\frac{m}{n}}{B_{R+}^\frac{m}{n}} }$。

  
  
• $\displaystyle{ \left(\frac{A_{R-}}{B_{R-}}\right)^\frac{m}{n} = \frac{A_{R-}^\frac{m}{n}}{B_{R-}^\frac{m}{n}} }$ （$n$ は奇数）

  $(A_{R-}C_{R-})^\frac{m}{n} = A_{R-}^{\frac{m}{n}}C_{R-}^\frac{m}{n}$ は成立していたので、上と同じように計算すればよろし。

  
  
• $\displaystyle{ \left(\frac{A_{R+}}{B_{R-}}\right)^\frac{m}{n} = \frac{A_{R+}^\frac{m}{n}}{B_{R-}^\frac{m}{n}} }$ （底の正負混在の場合。$n$ は奇数）

  $(A_{R+}C_{R-})^\frac{m}{n} = A_{R+}^{\frac{m}{n}}C_{R-}^\frac{m}{n}$ は成立していたので同様な計算でよろし。

$\square$ 有理数全体への拡張

これまでは、自然数を用いて有理数の指数 $\frac{m}{n}$ をあらわしてきた。 つまり正の有理数のみを考えてきたことになる。 一方で、基本指数法則が成り立つことも見てきた。 したがって負の有理数についても基本指数法則が成り立つことを求めれば、 \begin{align*} A_R^\frac{m}{n}A_R^{-\frac{m}{n}} = A_R^{\frac{m}{n} + (-\frac{m}{n})} = A_R^0 = 1 \end{align*} であるべき、ということになる。これを逆用して、 \begin{align*} A_R^{- \frac{m}{n}} \equiv \frac{1}{A_R^\frac{m}{n}} \end{align*} と定義する。 指数を自然数から整数にまで拡張したときと同様の考え方である。 もちろんこれには、$A_R^\frac{m}{n}$ の存在条件 \eqref{eq.r.02} または \eqref{eq.r.03} のもとで、という条件がついている。 この定義から、 \begin{align*} A_R^{-\frac{m}{n}} = \frac{1}{A_R^\frac{m}{n}} &= \frac{1}{\left(A_R^\frac{1}{n}\right)^m} = (A_R^\frac{1}{n})^{-m} \\ &= \frac{1}{\left(A_R^m\right)^\frac{1}{n}} = \frac{1^\frac{1}{n}}{\left(A_R^m\right)^\frac{1}{n}} = \left(\frac{1}{A_R^m}\right)^\frac{1}{n} = \left(A_R^{-m}\right)^\frac{1}{n} \end{align*} という関係も導き出せる。

指数が負の有理数の場合をこのように定義することによって、指数法則は有理数全体で成立することを示そう。 例によって $m,\, n,\, j,\, k$ は自然数であるとして、 \begin{align*} A_R^{-\frac{m}{n}}A_R^{-\frac{j}{k}} = \frac{1}{A_R^\frac{m}{n}} \cdot \frac{1}{A_R^\frac{j}{k}} = \frac{1}{A_R^\frac{m}{n}A_R^\frac{j}{k}} = \frac{1}{A_R^{\frac{m}{n}+\frac{j}{k}}} = A_R^{-(\frac{m}{n}+\frac{j}{k})} = A_R^{(-\frac{m}{n}) + (-\frac{j}{k})} \end{align*} となるから、指数が負の有理数どうしでも基本指数法則が成り立つことがわかる。 次に正の有理数と負の有理数が混じり合っている場合をみてみると \begin{alignat*}{2} A_R^{-\frac{m}{n} + \frac{j}{k}} = A_R^\frac{-mk + jn}{nk} = \left(A_R^\frac{1}{nk}\right)^{-mk + jn} &= \left(A_R^{\frac{1}{nk}}\right)^{-mk}\left(A_R^{\frac{1}{nk}}\right)^{jn} & &\quad\text{（$mk,\, jn$ は整数だから指数法則が使える）} \\ &= \frac{1}{\left(A_R^\frac{1}{nk}\right)^{mk}} \cdot \left(A_R^\frac{1}{nk}\right)^{jn} & & \\ &= \left. \left(A_R^\frac{1}{nk}\right)^{jn} \right/ \left(A_R^\frac{1}{nk}\right)^{mk} & & \\ &= \left(A_R^\frac{1}{nk}\right)^{jn - mk} & &\quad\text{（上と同じ理由）} \\ &= \left(A_R^\frac{1}{nk}\right)^{jn}\left(A_R^\frac{1}{nk}\right)^{-mk} & &\quad\text{（上と同じ理由）} \\ &= A_R^\frac{jn}{nk} A_R^{-\frac{mk}{nk}} & & \\ &= A_R^\frac{j}{k} A_R^{-\frac{m}{n}} & & \\ &= A_R^{-\frac{m}{n}} A_R^\frac{j}{k} & & \end{alignat*} であり、やはり基本指数法則は成り立っている。

また \begin{align*} (A_R B_R)^{-\frac{m}{n}} = \frac{1}{(A_R B_R)^\frac{m}{n}} = \frac{1}{A_R^\frac{m}{n} B_R^\frac{m}{n}} = \frac{1}{A_R^\frac{m}{n}} \cdot \frac{1}{B_R^\frac{m}{n}} = A_R^{-\frac{m}{n}} \cdot B_R^{- \frac{m}{n}} \end{align*} であるから、この指数法則も問題ない。

さらに。 \begin{align*} \left(A_R^{-\frac{m}{n}}\right)^{-\frac{j}{k}} = \left(\frac{1}{A_R^\frac{m}{n}}\right)^{-\frac{j}{k}} = \frac{1}{\left(\frac{1}{A_R^\frac{m}{n}}\right)^\frac{j}{k}} = \frac{1}{\frac{1}{A_R^\frac{mj}{nk}}} = A_R^\frac{mj}{nk} \end{align*} であり、 \begin{align*} & \left(A_R^{-\frac{m}{n}}\right)^\frac{j}{k} = \left(\frac{1}{A_R^\frac{m}{n}}\right)^\frac{j}{k} = \frac{1}{\left(A_R^\frac{m}{n}\right)^\frac{j}{k}} = \frac{1}{A_R^\frac{mj}{nk}} = A_R^{- \frac{mj}{nk}} \;, \\ & \left(A_R^\frac{m}{n}\right)^{-\frac{j}{k}} = \frac{1}{\left(A_R^\frac{m}{n}\right)^\frac{j}{k}} = \frac{1}{A_R^\frac{mj}{nk}} = A_R^{- \frac{mj}{nk}} \end{align*} となるから、指数に負の有理数を持ってきても問題なく成立している。

$\square$ 別の記法の導入

往々にして、$A_R^\frac{1}{n}$ は根号記号を使って $\sqrt[n]{A_R}$ と表記されることがある。 それゆえに、$A_R^\frac{m}{n}$ の存在条件 \eqref{eq.r.02}\eqref{eq.r.03} のもとで $\displaystyle{ A_R^\frac{m}{n} = (A_R^m)^\frac{1}{n} = \left(A_R^\frac{1}{n}\right)^m }$ であるから \begin{align*} \sqrt[n]{A_R^m} = \left(\sqrt[n]{A_R}\right)^m \end{align*} も成立する。 さらに、$n=2$ の場合は記述しない、という慣習もある。

いくつかの具体例をあげておこう： \begin{align*} & 2^{\frac{1}{2}} = \sqrt[2]{2} = \sqrt{2} \;, \quad 4^{\frac{1}{2}} = \sqrt{4} = 2 \;, \quad (2\pi)^{\frac{1}{2}} = \sqrt{2\pi} \;, \quad \pi^{\frac{1}{4}} = \sqrt[4]{\pi} \;, \\ & 2^{\frac{1}{3}} = \sqrt[3]{2} \;, \quad 27^{\frac{1}{3}} = \sqrt[3]{27} = 3 \;, \quad (-27)^{\frac{1}{3}} = \sqrt[3]{-27} = -3 \;, \\ & 2^{\frac{2}{3}} = \sqrt[3]{2^2} = \sqrt[3]{4} \;, \quad 2^{\frac{2}{3}} = \left(\sqrt[3]{2}\right)^2 = \sqrt[3]{4} \;, \\ & 8^{\frac{2}{3}} = \sqrt[3]{8^2} = \sqrt[3]{64} = 4 \;, \quad 8^{\frac{2}{3}} = \left(\sqrt[3]{8}\right)^2 = 2^2 = 4 \;, \\ & (-8)^{\frac{2}{3}} = \sqrt[3]{(-8)^2} = \sqrt[3]{64} = 4 \;, \quad (-8)^{\frac{2}{3}} = \left(\sqrt[3]{(-8)}\right)^2 = (-2)^2 = 4 \;, \\ & 2^{\frac{3}{2}} = \sqrt[2]{2^3} = \sqrt{8} = 2\sqrt{2}\;, \quad 4^{\frac{3}{2}} = \sqrt[2]{4^3} = \sqrt{64} = 8 \;. \end{align*} もちろん $\sqrt{-2}$ や $\sqrt[4]{-\pi}$ は実数の範囲では存在しない。

$\square$ まとめ

$n,\, m$ は自然数、$s,\, t$ は有理数である。

• 条件

  底 $A,\, B$ はともに実数で $0$ ではない。 それを明示する意味で、$A_R,\, B_R$ などと書く。

• 存在条件

  \begin{align*} \left. \begin{aligned} \text{$n,\, m$ は任意の自然数で} &\;\Rightarrow\; \left(A_{R+}^\frac{1}{n}\right)^m = \left(A_{R+}^m\right)^\frac{1}{n} = A_{R+}^\frac{m}{n} \\ \text{$n$ が奇数、$m$ は任意の自然数で} &\;\Rightarrow\; \left(A_{R-}^\frac{1}{n}\right)^m = \left(A_{R-}^m\right)^\frac{1}{n} = A_{R-}^\frac{m}{n} \end{aligned} \right\} \end{align*}

• 定義

  存在条件を前提としているので、$A_{R+},\, A_{R-}$ の区別なく成立するものは $A_R$ でまとめてあらわす。 \begin{align*} & A_R^n \equiv \overbrace{A_R \cdot A_R \cdot A_R \cdot \cdots \cdot A_R}^{n\; \text{個}} \\ & A_R^1 \equiv A_R \\ & A_R^0 \equiv 1 \\ & A_R^\frac{1}{n} \equiv \sqrt[n]{A_R} \quad\text{は $A_{R}$ の 実数の $n$ 乗根を表す} \\ & A_{R+}^\frac{1}{n} \equiv \sqrt[n]{A_{R+}} \quad\text{は $A_{R+}$ の 実数の $n$ 乗根で正のものを表す} \\ & A_R^{-s} \equiv \frac{1}{A_R^s} \end{align*}

• 基本指数法則 \begin{align*} A_R^{s+t} = A_R^s A_R^t \end{align*}
• 指数法則 \begin{align*} & (A_R B_R)^s = A_R^s B_R^s = B_R^s A_R^s \\ & (A_R^s)^t = (A_R^t)^s = A_R^{st} = A_R^{ts} \\ \end{align*}
• 付随的指数法則（覚えるまでもないが、覚えておいても損はない） \begin{align*} & A_R^{s-t} = \frac{A_R^s}{A_R^t} \\ & A_R^{-s} = \frac{1}{A_R^s} = \left(\frac{1}{A_R}\right)^s \;\iff\; \left(\frac{1}{A_R}\right)^{-s} = A_R^s \\ & \left(\frac{A_R}{B_R}\right)^s = \frac{A_R^s}{B_R^s} \;\iff\; \left(\frac{A_R}{B_R}\right)^{-s} = \left(\frac{B_R}{A_R}\right)^s = \frac{B_R^s}{A_R^s} \end{align*}

---

実数の世界

$\square$ 無理数の指数

前の節で、指数表記の底が実数で指数が有理数のときの指数法則の成り立ち具合をみてきた。 したがって、指数が無理数の場合が考察できれば、指数を実数全体に拡張したときの指数法則の生態が判明すると期待できる。 一方で底についてはどうだろうか？ 指数が有理数である数においては、底を実数に限らなければ考察が進められなかった。 有理数の場合でそうなのであるから、無理数の場合でもそれは踏襲されるべきだろうと想像できる。 いったん問題を「縮小」したのだから、今更拡大してもしょうがあるまい。

$A_{R+}^\sqrt{2}$ という数を考えよう。 といってもどう考えれば良いのか。 $A_{R+}^\pi$ もしかり。 どう考えれば良いのか？ そもそも存在して、かつ、一つの数という実体が定まるのか？ 有理数の指数までは、ひとつひとつと数え上げられる自然数 $n$ と、$n$ 回掛け合わせるという掛け算の概念だけで（ほぼ）まかなえてきた。 ただ、$n$ 乗根にまつわる考察で、解析学の力を借りた。 なので、ここでも同様に、解析学の力を借りてみる。

解析学によれば、無理数 $u$ は、有理数の列 $s_1, s_2, \ldots, s_n, \ldots$ の極限として定義することが可能である（そのような有理数の列が存在する、ということ）。 すなわち、 \begin{align*} u = \lim_{n \to \infty} s_n \end{align*} これを指数に当てはめれば、形として \begin{align*} A_{R+}^u = \lim_{n \to \infty} A_{R+}^{s_n} = A_{R+}^{\lim_{n \to \infty} s_n} \end{align*} という仰々しいものになる。 極限操作の途中経過を記してみると、 \begin{align*} A_{R+}^u &\sim A_{R+}^{s_n} \\ A_{R+}^u &\sim A_{R+}^{s_{n+1}} \\ \cdots&\cdots\cdots \end{align*} であり、徐々に $A_{R+}^u$ に近づいていくことが透けて見える。 また、すでに有理数指数の $A_{R+}^{s_n}$ の存在は確かめられているので、極限においても数が存在してかつひとつの数に定まるように感じられてくる。 そしてそれは、結論からいえば、正しい。

なお、ここで正の実数 $A_{R+}$ に限定しているのは細工ではなく、それなりの意味がある。 そもそもとして、負の数の無理数乗を考えることに無理があるのである。 $-1$ には偶数回かければ正、奇数回かければ負という性質（偶奇性）があり、整数、有理数は、自然数を使って組み立てることができたので、偶奇性を用いての考察も可能なのであった。 $A_{R-}$ に対する有理数乗では、分母が奇数でないまずい、といった考察である。 しかしながら、無理数は自然数を使ってあらわすことが不可能である。 それゆえ、無理数に対しては、偶数・奇数という分別は存在しない。 したがって、$(-1)^u$ は考察不能であり、偶奇性を考慮しなくて済む正の実数 $A_{R+}$ に限定しなくては、手が出せないのである。 もはや、回数という概念はなりたたない。

$\square$ はじめに指数関数ありき

解析学の力を借りることを決心したのだから、思い切って、指数関数 $e^x$ を利用してことにあたることにする。

まず最初に、$e$ は正の実数であること、$x,\, u$ は実数であることに留意しておこう。 そのうえで指数関数は \begin{align*} e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \cdots = \sum_{n=0}^\infty\frac{x^n}{n!} \quad(0! \equiv 1) \;. \end{align*} と定義され、かつ導関数が元の関数と変わらないという性質 \begin{align*} \frac{d}{dx}e^x = e^x \quad \therefore \; \frac{d^n}{dx^n}e^x = e^x \end{align*} がある。 そのうえ指数関数であるのだから \begin{align*} \left. \frac{d^n}{dx^n}e^x \right|_{x=0} = e^0 = 1 \quad (\text{for all }n) \end{align*} となる。 このような指数関数の $e$ は $e \simeq 2.718\cdots$ というネイピア数であることは著名な事実である。

次に、$e^{x + u}$ を $u$ の周りでテーラー展開する。一般に \begin{align*} f(x+u) = f(x) + \frac{f^\prime(x)}{1!}u + \frac{f^{\prime\prime}(x)}{2!}u^2 + \cdots = \sum_{n=0}^\infty \frac{f^{(n)}(x)}{n!}u^n \end{align*} であるから、$f(x) = e^x$ とすると $f^{(n)}(x) = e^x = f(x)$ でもあるので \begin{align*} f(x+u) = \sum_{n=0}^\infty \frac{f^{(n)}(x)}{n!}u^n = \sum_{n=0}^\infty \frac{f(x)}{n!}u^n = f(x) \sum_{n=0}^\infty \frac{u^n}{n!} = f(x)f(u) \iff e^{x+u} = e^xe^u \end{align*} となる。 この結果から、指数関数は、指数が実数の場合においても基本指数法則を満たしていることがわかる。 それゆえ $e^{-x}$ が \begin{align*} e^x e^{-x} = e^{x-x} = e^0 = 1 \iff e^{-x} = \frac{1}{e^x} \end{align*} で与えられることになる。 $x$ が無理数でもこの関係は成り立つのである。

$\square$ 対数関数（指数関数の逆関数）

指数関数 $e^x$ は、$e^x \gt 0\; (\text{for all }x)$ でありかつ単調増加関数という性質を持つので、逆関数が存在する。 それを対数関数といい、$\log_e$ という名前で定義する。すなわち \begin{align*} y = e^x \iff x = \log_e{y} \;. \end{align*} このように定義したのだから、当然 $y \gt 0$ である。 「対数の真数は正」というスローガンはここから生まれてくる。 また、この定義の左右を組み合わせれば次のような「１回ひねり」的な結果が得られる： \begin{align*} y = e^{\log_e{y}}\;, \quad x = \log_e{e^x} \;. \end{align*} $y_1 = e^{x_1},\; y_2 = e^{x_2}$ とすると、$e^{x_1}e^{x_2} = e^{x_1 + x_2}$ という基本指数法則を使えば \begin{align*} \log_e(y_1 y_2) = \log_e(e^{x_1}e^{x_2}) = \log_e{e^{x_1 + x_2}} = x_1 + x_2 = \log_e{y_1} + \log_e{y_2} \end{align*} という結果も得られる。 $\displaystyle{ \log_e\left(\frac{y_1}{y_2}\right) }$ についても \begin{align*} \log_e\left(\frac{y_1}{y_2}\right) = \log_e\left(\frac{e^{x_1}}{e^{x_2}}\right) = \log_e\left({e^{x_1} e^{-x_2}}\right) = \log_e{e^{x_1 - x_2}} = x_1 - x_2 = \log_e{y_1} - \log_e{y_2} \end{align*} という結果になる。 「掛け算が足算に」「割り算が引き算に」という対数の特徴である。

往々にして「両辺の対数をとる」という操作が行われることがある。 上と同様に $y_1 = e^{x_1},\; y_2 = e^{x_2}$ とし、その上で $y_1 = y_2$ となるときを考えると \begin{align*} y_1 = y_2 \iff e^{x_1} = e^{x_2} \iff x_1 = x_2 \iff \log_e{y_1} = \log_e{y_2} \end{align*} となって、対数をとっても等しいことに変わりがない。 つまり正の数どうしの等式においては、両辺の対数をとっても等しいのである。

さらに $e^0 = 1$ という事実から \begin{align*} \log_e{1} = 0 \end{align*} という特徴的な関係があることを付け加えておこう。

$\square$ 一般の指数関数、冪乗関数

今、仮に、$a^x = e^{x \log_e{a}}$ であるとしよう（もちろん $a \gt 0$ である）。 この仮定は、$a = e^{\log_e{a}}$ の両辺を $x$ 乗して \begin{align*} a^x = \left(e^{\log_e{a}}\right)^x = e^{x \log_e{a}} \end{align*} という式変形から導かれた仮定である。 けれども、そもそも今は、指数が実数のときの指数法則を考察しているので、この式変形で用いた $\left(e^{\log_e{a}}\right)^x = e^{x \log_e{a}}$ を無条件に認めて使用するわけには行かない。 何らかの方法で、この変形が成り立つことを言わねばならない。 天下りは許されないのである。

ここで、正の実数 $h$ を用いて $g(x) = e^{hx}$ という関数をわざと考える。 このとき \begin{align*} g(x+u) = e^{h(x+u)} = e^{hx}e^{hu} = g(x)g(u) \end{align*} であるから $g(x)$ は基本指数法則を満たしている（指数関数 $e^x$ が基本法則を満たすことを利用した）。 これを続けることによって \begin{align*} g(x_1 + x_2 + \cdots + x_n) = g(x_1)g(x_2) \cdots g(x_n) \end{align*} となる。 $x_1 = x_2 = \cdots = x_n = 1$ という特別な場合を考え、かつ、$a := g(1) = e^h \;(\gt 0)$ とすると \begin{align*} g(n) = (g(1))^n = a^n \end{align*} という関係が得られる。

ひとつ飛躍をする。 この関係式は自然数 $n$ での関係を述べたものであるが、そもそも関数 $g$ は $g(x) = e^{hx}$ として実数を変数とする指数関数を用いて導入されたものであった。 それゆえこの関係を実数 $x$ にまで拡張しても問題なかろうとしてしまうのである。 この飛躍の結果、$g(x) = a^x$ となる。 そして、そもそもの $g(x) = e^{hx}$ と $a = g(1) = e^h \iff h = \log_e{a}$ から \begin{align*} g(x) = a^x = e^{hx} = e^{x \log_e{a}} \end{align*} とすることができる。 これをもって、一般の指数関数 $a^x$ の定義とする。冒頭の仮定がそれなりにもっともらしくなってくる。

$g(x)$ が基本指数法則を満たしていたことから、このように定義された一般の指数関数 $a^x$ も、実数の指数において、基本指数法則を満たしている。 また、$h$ は正の実数であればなんでも良かったので、当然 $a$ も正の実数すべてをカバーしている。 さらに \begin{align*} a^1 = e^{1 \cdot \log_e a} = e^{\log_e a} = a \end{align*} という結果も得られる（この理路を、かの有名な『解析概論』（高木貞治著）から学んだ。参照したのは、改訂第三版第19刷（岩波書店））。

$a^x = e^{x \log_e{a}}$ であるから、対数関数の定義により \begin{align*} \log_e{a^x} = \log_e{e^{x \log_e{a}}} = x\log_e{a} \end{align*} である（もちろん、両辺の対数をとって導いてもいい）。

$a^x$ において　$a$ と $x$ の役割を交換すると \begin{align*} x^a = e^{a \log_e{x}} \end{align*} となる。 これを $x$ の関数と捉えたものが、冪乗関数といわれるものである。

$\square$ 指数法則の確認

一般の指数関数、そして冪乗関数は、先に見たように、基本指数法則を満たしていた。 また、これらの関数は、何を変数と見るかが異なるだけで、形式は同じであった。 それを受けて、ここからは $A_{R+}^u$ という形式で指数法則をみていってみることにする。 $u$ は実数全体をカバーする数（当然無理数を含む）である。

これまでの考察から \begin{align*} & A_{R+}^u = e^{u \log_e{A_{R+}}} \;, \\ & \log_e{(A_{R+} B_{R+})} = \log_e{A_{R+}} + \log_e{B_{R+}} \;, \\ & \log_e{A_{R+}^u} = \log_e{e^{u \log_e{A_{R+}}}} \;, \end{align*} ということが成り立つことがわかっている。

まず基本指数法則をおさらいすると、 \begin{align*} A_{R+}^u A_{R+}^v = e^{u \log_e{A_{R+}}} e^{v \log_e{A_{R+}}} = e^{u \log_e{A_{R+}} + v \log_e{A_{R+}}} = e^{(u + v) \log_e{A_{R+}}} = A_{R+}^{u+v} \;. \end{align*} $(A_{R+}B_{R+})^u = A_{R+}^u B_{R+}^u$ は次のように示される： \begin{align*} (A_{R+}B_{R+})^u = e^{u \log_e{(A_{R+}B_{R+})}} = e^{u (\log_e{A_{R+}} + \log_e{B_{R+})}} = e^{u \log_e{A_{R+}}} e^{u \log_e{B_{R+}}} = A_{R+}^u B_{R+}^u \;. \end{align*} $(A_{R+}^u)^v = A_{R+}^{uv}$ については \begin{align*} (A_{R+}^u)^v = e^{v \log_e{A_{R+}^u}} = e^{vu \log_e{A_{R+}}} = A_{R+}^{vu} = A_{R+}^{uv} \;. \end{align*}

指数が負の実数である場合は、指数関数のところでみた $e^{-x} = 1/e^x$ という関係を使って \begin{align*} A_{R+}^{-u} = e^{-u \log_e{A_{R+}}} = \frac{1}{e^{u \log_e{A_{R+}}}} = \frac{1}{A_{R+}^u} \end{align*} となる。 ここで $(1/A_{R+})^u$ を定義通りに実行すると \begin{align*} \left(\frac{1}{A_{R+}}\right)^u = e^{u \log_e{\left(\frac{1}{A_{R+}}\right)}} = e^{u (\log_e{1} - \log_e{A_{R+}})} = e^{- u \log_e{A_{R+}}} = \frac{1}{A_{R+}^u} \end{align*} であるから \begin{align*} A_{R+}^{-u} = \frac{1}{A_{R+}^u} = \left(\frac{1}{A_{R+}}\right)^u \;. \end{align*} この結果を利用することにより \begin{align*} \left(\frac{A_{R+}}{B_{R+}}\right)^u = A_{R+}^u \cdot \left(\frac{1}{B_{R+}}\right)^u = \frac{A_{R+}^u}{B_{R+}^u} \end{align*} も得られる。

背後に隠れている $1$ の実数乗について見ておこう。 今求めた指数法則を額面通りに使うと \begin{align*} \left(\frac{1}{A_{R+}}\right)^u = \left(1 \cdot \frac{1}{A_{R+}}\right)^u = 1^u \cdot \left(\frac{1}{A_{R+}}\right)^u \end{align*} となる。 これより $1^u = 1$ という事実が炙り出される。 この事実は \begin{align*} 1^u = e^{u \log_e 1} = e^0 = 1 \end{align*} という方向からも導き出せる。 すなわち、$1$ は実数乗しても（無理数乗が含まれていることは言うまでもなし）$1$ なのである（$1^\sqrt{2} = 1^{-\pi} = 1$ !!）。 安心してよい。

$\square$ まとめ

指数が実数の場合についてをまとめておこう。 $u,\, v$ は実数である。

• 条件

  底 $A,\, B$ はともに正の実数である（$0$ は含まない）。 それを明示する意味で、$A_{R+},\, B_{R+}$ などと書く。

• 定義 \begin{align*} & A_{R+}^u \equiv e^{u \log_e{A_{R+}}} \\ & A_{R+}^1 \equiv A_{R+} \\ & A_{R+}^0 \equiv 1 \\ \end{align*}
• 基本指数法則 \begin{align*} A_{R+}^{u+v} = A_{R+}^u A_{R+}^v \end{align*}
• 指数法則 \begin{align*} & (A_{R+} B_{R+})^u = A_{R+}^u B_{R+}^u = B_{R+}^u A_{R+}^u \\ & (A_{R+}^u)^v = (A_{R+}^v)^u = A_{R+}^{uv} = A_{R+}^{vu} \end{align*}
• 付随的指数法則（覚える必要はないが、覚えておいても損はない） \begin{align*} & A_{R+}^{u-v} = \frac{A_{R+}^u}{A_{R+}^v} \\ & A_{R+}^{-u} = \frac{1}{A_{R+}^u} = \left(\frac{1}{A_{R+}}\right)^u \;\iff\; \left(\frac{1}{A_{R+}}\right)^{-u} = A_{R+}^u \\ & \left(\frac{A_{R+}}{B_{R+}}\right)^u = \frac{A_{R+}^u}{B_{R+}^u} \;\iff\; \left(\frac{A_{R+}}{B_{R+}}\right)^{-u} = \left(\frac{B_{R+}}{A_{R+}}\right)^u = \frac{B_{R+}^u}{A_{R+}^u} \end{align*}

---

複素数の世界のさわり

$\square$ 今までの議論のおさらい

指数が自然数と整数の時には、指数法則は底となる数についての制限はなかった。 したがって、複素数 $z,\, w$ に対しても、$k,\, l$ を整数として \begin{align*} & z^{k+l} = z^k z^l \;, \\ & (zw)^k = z^k w^k = w^k z^k \;, \\ & (z^k)^l = (z^l)^k = z^{kl} = z^{lk} \end{align*} は成立することになると推測されるが、それは本当だろうか？

また指数を有理数にまで広げるとき、底については実数という制限がついた。指数を実数に拡張するときには、底は正の実数でなければならない、という条件がついた。 そうしないと問題が片付かなかった。 なので、底や指数が複素数のときを考える場合には、今までの議論の延長では無理だろう。 そもそも正の複素数とか負の複素数などはありえない。 そこで今度は、複素関数論（複素解析と言われたりもする）の分野の助けを借りて、考えていってみる。

$\square$ 複素指数関数と複素対数関数

これからの考察に必要な定義と関数を記そう。 以下、個別な事象の説明（または証明もどき）は省略していることがほとんどである。 なので、個人的で簡単なまとめを 「複素｛指数関数、対数関数｝の世界のさわり」 というタイトルの別稿として記した。 以下で述べる計算の詳細に疑問がある場合には、そちらも参照してもらいたい。 もちろんよい教科書にあたることが大前提で必要です。

複素数の定義

最初に複素数を定義しよう。 $x, y$ は実数、$i$ は虚数単位（すなわち $i^2 = -1$）として \begin{align*} z \equiv x + iy \end{align*} という形式であらわされる数を複素数という。 $y = 0$ ならばそれは実数である。$y \neq 0$ のときには「虚数」と言われる。

複素指数関数

次に複素指数関数である。 これは \begin{align*} e^z = \sum_{n=0}^\infty \frac{z^n}{n!} \quad(0! \equiv 1) \end{align*} と定義される。 ここですでに $z^n$ という複素数の自然数乗があらわれてきているが、生い立ちのところでみたように、$z$ を $n$ 回掛けるという単なる掛け算のことを意味している。 またこの複素指数関数の導関数には \begin{align*} \frac{de^z}{dz} = e^z \end{align*} という事実があって、それゆえ $n$ 階導関数も $e^z$ になる。 この結果と複素関数でのテーラ展開を用いると \begin{align*} e^{z+w} = e^z e^w \end{align*} という基本指数法則が成り立つことが導出できる（$w$ も複素数である）。 それゆえ、$w = -z$ とすることにより、 \begin{align*} e^{z-z} = 1 \iff e^{-z} = \frac{1}{e^z} \end{align*} となる。

そしてさらに、$\theta$ を実数として $e^{i\theta}$ を考えマクローリン展開を施すと \begin{align*} e^{i\theta} = \cos\theta + i\sin\theta \end{align*} という関係が導出できる。 以上の結果と複素平面という幾何学的な描像を利用して、複素数のもう一つの表現方法 \begin{align*} z = x + iy = re^{i\theta} = r(\cos\theta + i\sin\theta) \;, \quad \begin{cases} x = r\cos\theta, \; y = r\sin\theta \\ r = \sqrt{x^2 + y^2} \\ \theta = tan^{-1}\dfrac{y}{x} \end{cases} \end{align*} が得られる。 $r,\, \theta$ には名前がついていて \begin{align*} r &\;:\; \text{複素数 $z$ の絶対値。$\abs{z}$ とも書く。} \\ \theta &\;:\; \text{複素数 $z$ の偏角。} \\ \end{align*} と言われる。

偏角関数

三角関数の性質から明らかなように、この偏角 $\theta$ はひとつには決まらない。 それらをまとめて $\arg(z)$ と書く（$z$ の偏角を与える関数と捉えても良い）： \begin{align*} \arg(z) = \theta + 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \;. \end{align*} この偏角関数を利用することによって、複素数 $z$ それ自身で複素数が表記できることになる： \begin{align*} z = \abs{z}e^{i\cdot \arg(z)} \;. \end{align*}

偏角関数には次の性質がある： \begin{align*} & \arg(zw) = \arg(z) + \arg(w) \;, \\ & \arg\left(\frac{z}{w}\right) = \arg(z) - \arg(w) \;. \end{align*}

複素対数関数

複素対数関数は $w = e^z$ を元にしてその逆関数を考えることにより \begin{align*} w = e^z \iff \mathbb{log}_e{w} = z \end{align*} とひとまず定義する（実数までの世界での対数関数 $\log_e$ と区別するために、$\mathbb{log}_e$ という記号を使った）。 ここで $e^z$ の周期性 \begin{align*} e^{z + i\cdot 2\pi} = e^z e^{i\cdot 2\pi} = e^z \end{align*} から $\mathbb{log}_e{w}$ には不定性があることがわかる。 これをまとめて（先の $\arg$ のように） \begin{align*} \mathbb{log}_e{w} = z + i\cdot 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \end{align*} と書く。 $w = e^z$ と起き戻せば、意外にも \begin{align*} \mathbb{log}_e{e^z} = z + i\cdot 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \end{align*} ということになって、意表をつかれる。 実数までの対数関数の常識は通じなくなるのである。

さらにここで $w = \abs{w}e^{i\cdot \arg(w)}$ という表現を使うと、 \begin{align*} w = \abs{w}e^{i\cdot \arg(w)} = e^{\log_e\abs{w}}e^{i\cdot \arg(w)} = e^{\log_e\abs{w} + i\cdot \arg(w)} \end{align*} であるから、複素対数関数の定義によって \begin{align*} \mathbb{log}_e{w} = \log_e{\abs{w}} + i\cdot \arg(w) \end{align*} という結果も得られる。 この結果を利用することによって、対数の基本的な法則は、複素数の世界でも成り立っていることが導出できる。 すなわち \begin{align*} \mathbb{log}_e{z} + \mathbb{log}_e{w} & = \left(\log_e{\abs{z}} + i\cdot \arg(z)\right) + \left(\log_e{\abs{w}} + i\cdot \arg(w)\right) \\ & = \left(\log_e{\abs{z}} + \log_e{\abs{w}}\right) + \left(i\cdot \arg(z) + i\cdot \arg(w)\right) \\ & = \log_e{\abs{zw}} + i\cdot \arg(zw) \\ & = \mathbb{log}_e{(zw)} \;. \end{align*} ほぼ同様にして \begin{align*} \mathbb{log}_e{z} - \mathbb{log}_e{w} & = \left(\log_e{\abs{z}} + i\cdot \arg(z)\right) - \left(\log_e{\abs{w}} + i\cdot \arg(w)\right) \\ & = \left(\log_e{\abs{z}} - \log_e{\abs{w}}\right) + \left(i\cdot \arg(z) - i\cdot \arg(w)\right) \\ & = \log_e{\abs{\frac{z}{w}}} + i\cdot \arg\left(\frac{z}{w}\right) \\ & = \mathbb{log}_e{\left(\frac{z}{w}\right)} \;. \end{align*}

$\square$ 一般の複素指数関数と複素冪乗関数

まずはじめに次の定義を認めることとしよう（$\alpha,\, \beta$ は複素数）： \begin{align*} \alpha^\beta \equiv e^{\beta \cdot \mathbb{log}_e \alpha} \quad(\alpha \neq 0) \end{align*} これは実数までの世界の一般の指数関数や冪乗関数からの無条件の演繹である。 この形式において何を変数とみるかで、一般の複素指数関数と複素冪乗関数が区別される。 すなわち、 \begin{align*} \text{一般の複素指数関数} &\;:\; f(z) = \alpha^z = e^{z \cdot \mathbb{log}_e \alpha} \\ \text{複素冪乗関数} &\;:\; g(z) = z^\beta = e^{\beta \cdot \mathbb{log}_e z} \end{align*} 形式は同じなので、代数的操作はどちらについても変わらない。 ただし、不定性の原因は異なる。 $\alpha^z$ の不定性は、$\alpha$ の偏角の不定性によるものであり、$z^\beta$ の不定性は、$z$ の偏角の不定性によるものである。 これは実数までの世界ではあらわれてこない事柄である。

さらに \begin{align*} \mathbb{log}_e \alpha^\beta = \beta \mathbb{log}_e \alpha + i\cdot 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \end{align*} という事実も判明している。

$\square$ 指数法則の確認

これまで見てきた指数法則が複素数の場合にどうなるかを確認してみる。 忘れてならない基本は、複素指数関数 $e^z$ においては $e^{z+w} = e^ze^w$ という基本指数法則が成立するという事実と、それの裏返しである $\mathbb{log}_e(zw) = \mathbb{log}_e{z} + \mathbb{log}_e{w}$ が成立するという事実である。 そして $\arg(z)$ と $\mathbb{log}_e{z}$ の不定性である。

$\bullet\; \alpha^{\beta + \gamma} = \alpha^\beta \alpha^\gamma$ は成立するか？

\begin{align*} \alpha^{\beta + \gamma} &= e^{(\beta + \gamma) \cdot \mathbb{log}_e{\alpha}} = e^{(\beta + \gamma) \cdot (\log_e{\abs{\alpha}} + i\cdot \arg(\alpha))} \\ &= e^{(\beta + \gamma) \cdot \log_e{\abs{\alpha}}} e^{i\cdot (\beta + \gamma) \cdot \arg(\alpha)} \\ \alpha^\beta \alpha^\gamma &= e^{\beta \cdot \mathbb{log}_e{\alpha}} e^{\gamma \cdot \mathbb{log}_e{\alpha}} = e^{\beta\cdot(\log_e{\abs{\alpha}} + i\cdot \arg(\alpha))} e^{\gamma\cdot(\log_e{\abs{\alpha}} + i\cdot \arg(\alpha))} \\ &= e^{\beta\cdot\log_e{\abs{\alpha}}} e^{i\cdot \beta \cdot \arg(\alpha)} e^{\gamma\cdot\log_e{\abs{\alpha}}} e^{i\cdot \gamma \cdot \arg(\alpha)} \\ &= e^{(\beta + \gamma)\cdot\log_e{\abs{\alpha}}} e^{i\cdot(\beta \cdot \arg(\alpha)+ \gamma \cdot \arg(\alpha))} \;, \end{align*} である。 さてここで偏角には不定性があったことを思い出そう。 $\arg(\alpha)$ には、無限の個数の候補があって、その中からどれを選ぶかは全くもって任意なのである。したがって一般には \begin{align*} (\beta + \gamma) \cdot \arg(\alpha) \neq \beta \cdot \arg(\alpha)+ \gamma \cdot \arg(\alpha) \end{align*} なのである。 そこで、ひとつ高いところからの規範として、$\alpha$ の偏角として常に同じものを採用する、という制限を課してみよう。 同じものを採用するということの意味は、$\arg(\alpha) = \theta + 2k\pi \;\;(k = 0, \pm 1, \pm 2, \ldots)$ とあらわしたうえで、上記の $\arg$ 各々にそれぞれ別の $k$ を用意すれば \begin{align*} (\beta + \gamma) \cdot \arg(\alpha) = (\beta + \gamma) \cdot (\theta + 2k\pi) &= (\beta + \gamma) \cdot \theta + \beta \cdot 2k\pi + \gamma \cdot 2k\pi \;, \\ \beta \cdot \arg(\alpha)+ \gamma \cdot \arg(\alpha) = \beta \cdot (\theta + 2k^\prime \pi) + \gamma \cdot (\theta + 2k^{\prime\prime}\pi) &= (\beta + \gamma) \cdot \theta + \beta \cdot 2k^\prime\pi + \gamma \cdot 2k^{\prime\prime}\pi \end{align*} となるので、ここで $k = k^\prime = k^{\prime\prime}$ とする、ということである。 そしてそのときには \begin{align*} (\beta + \gamma) \cdot \arg(\alpha) = \beta \cdot \arg(\alpha)+ \gamma \cdot \arg(\alpha) \end{align*} となって、その場合に限り $\alpha^\beta \alpha^\gamma = \alpha^{\beta + \gamma}$ は成り立つのである。

このように、不定性を持つ $\arg$ 関数についての演算が式の中に出てきた場合には常に同様の留意を払わねばならない（$\mathbb{log}_e$ についてもしかり）。 しからば、そもそもの複素指数関数の基本指数法則 $e^ze^w = e^{z + w}$ はなぜ成り立っていたのか？ 実は $e^z$ には、$e$ の偏角として常に同じものを用いるという掟が隠されていたのである（$\arg(e) = 2k\pi$ で常に同じものを使う。そしてそれは往々にして、$k = 0$ のときの $\arg(e) = 0$）。先に言ってほしいぜよ。

$\bullet\; (\alpha\beta)^\gamma = \alpha^\gamma \beta^\gamma$ は成立するか？

\begin{align*} (\alpha\beta)^\gamma = e^{\gamma\cdot\mathbb{log}_e{(\alpha\beta)}} = e^{\gamma\cdot(\mathbb{log}_e{\alpha} + \mathbb{log}_e{\beta})} = e^{\gamma\cdot\mathbb{log}_e{\alpha}} e^{\gamma\cdot\mathbb{log}_e{\beta}} = \alpha^\gamma \beta^\gamma \end{align*} となり間違いなく成立することが言える（最終形に不定性を持つ関数が現れてきていないので問題はない）。

ほぼ同様にして \begin{align*} \left(\frac{\alpha}{\beta}\right)^\gamma = e^{\gamma\cdot\mathbb{log}_e{\left(\frac{\alpha}{\beta}\right)}} = e^{\gamma\cdot(\mathbb{log}_e{\alpha} - \mathbb{log}_e{\beta})} = \frac{e^{\gamma\cdot\mathbb{log}_e{\alpha}}}{e^{\gamma\cdot\mathbb{log}_e{\beta}}} = \frac{\alpha^\gamma}{\beta^\gamma} \;. \end{align*}

$\bullet\; \left(\eta^\alpha\right)^\beta$ と $\left(\eta^\beta\right)^\alpha$ と $\eta^{\alpha\beta}$ の関係はどうか？

各々を計算していってみると（$k,, k^\prime = 0, \pm 1 \pm2 \ldots$） \begin{align*} \left(\eta^\alpha\right)^\beta &= e^{\beta \cdot \mathbb{log}_e{\eta^\alpha}} = e^{\beta \cdot (\alpha \cdot \mathbb{log}_e{\eta} + i\cdot 2k\pi)} = e^{\alpha\beta \cdot \mathbb{log}_e{\eta}} e^{i\cdot \beta \cdot 2k\pi} \;, \\ \left(\eta^\beta\right)^\alpha &= e^{\alpha \cdot \mathbb{log}_e{\eta^\beta}} = e^{\alpha \cdot (\beta \cdot \mathbb{log}_e{\eta} + i\cdot 2k^\prime\pi)} = e^{\alpha\beta \cdot \mathbb{log}_e{\eta}} e^{i\cdot \alpha \cdot 2k^\prime\pi} \;, \\ \eta^{\alpha\beta} &= e^{\alpha\beta \cdot \mathbb{log}_e{\eta}} \end{align*} という結果を得る。 一般的にはこれらは等しくはない。 しかしながら、仮に $\alpha,\, \beta$ が整数であった場合には事情がかわる。 $\alpha = l,\, \beta = j$（$l, j$ は整数）と置き換えると、$k^\prime l,\, kj$ ともに整数であるから \begin{align*} & e^{i\cdot \beta \cdot 2k\pi} = e^{i\cdot 2kj\pi} = 1 \;, \\ & e^{i\cdot \alpha \cdot 2k^\prime\pi} = e^{i\cdot 2k^\prime l\pi} = 1 \end{align*} となり、その結果 \begin{align*} \left(\eta^l\right)^j &= e^{lj \cdot \mathbb{log}_e{\eta}} \;, \\ \left(\eta^j\right)^l &= e^{lj \cdot \mathbb{log}_e{\eta}} \;, \\ \eta^{lj} &= e^{lj \cdot \mathbb{log}_e{\eta}} \end{align*} を得る。 したがって \begin{align*} \left(\eta^l\right)^j = \left(\eta^j\right)^l = \eta^{lj} \end{align*} が成立する。 整数でない場合には、この式は成立しない。

$\square$ $\alpha^\beta$ の研究

$\alpha^\beta = e^{\beta\cdot \mathbb{log}_e{\alpha}}$ を元にして、少し研究をしてみよう。

$\bullet\; \alpha^{-1} = \dfrac{1}{\alpha}$

$\alpha$ は \begin{align*} \alpha = e^{\mathbb{log}_e{\alpha}} = e^{\log_e{\abs{\alpha}} + i\cdot \arg(\alpha)} = e^{\log_e{\abs{\alpha}} + i\cdot (\theta + 2k\pi)} = e^{\log_e{\abs{\alpha}}} e^{i\theta} e^{i\cdot 2k\pi} = e^{\log_e{\abs{\alpha}}} e^{i\theta} \end{align*} とあらわせる。 一方で、$\alpha^{-1}$ は \begin{align*} \alpha^{-1} = e^{-\mathbb{log}_e{\alpha}} = e^{-\log_e{\abs{\alpha}} - i\cdot \arg(\alpha)} = e^{-\log_e{\abs{\alpha}} - i\cdot (\theta + 2k\pi)} = e^{-\log_e{\abs{\alpha}}} e^{-i\theta} e^{-i\cdot 2k\pi} \end{align*} となる。 $e^{-z} = 1/e^z$ であったから、もちろん $e^{-i\theta} = 1/e^{i\theta}$ であり、また $e^{-i\cdot 2k\pi} = 1/e^{i\cdot 2k\pi} = 1$ であるから、 \begin{align*} \alpha^{-1} = e^{-\log_e{\abs{\alpha}}}\frac{1}{e^{i\theta}} \end{align*} となる。 さらに $e^{-\log_e{\abs{\alpha}}}$ は実対数関数であるから躊躇なく $\displaystyle{e^{-\log_e{\abs{\alpha}}} = 1/e^{\log_e{\abs{\alpha}}}}$ と計算ができて、 \begin{align*} \alpha^{-1} = e^{-\log_e{\abs{\alpha}}} \frac{1}{e^{i\theta}} = \frac{1}{e^{\log_e{\abs{\alpha}}} e^{i\theta}} = \frac{1}{\alpha} \end{align*} という結果が得られる。

$\bullet\; \mathbb{log}_e{\alpha^{-1}} = \mathbb{log}_e{\dfrac{1}{\alpha}} = -\mathbb{log}_e{\alpha}$

$\alpha^\beta$ の複素対数は、前にも述べたように \begin{align*} \mathbb{log}_e{\alpha^\beta} = \beta \mathbb{log}_e{\alpha} + i\cdot 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \end{align*} であった。 ここで $\beta = -1$ の場合には \begin{align*} \mathbb{log}_e{\alpha^{-1}} = - \mathbb{log}_e{\alpha} + i\cdot 2k\pi \end{align*} となる。 考察を深めるために、$\mathbb{log}_e{\alpha}$ を実部と虚部に分解しよう。 実際 \begin{align*} \mathbb{log}_e{\alpha} = \log_e{\abs{\alpha}} + i\cdot\arg(\alpha) = \log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2k^\prime\pi \quad(k^\prime = 0, \pm 1, \pm 2, \ldots) \end{align*} であるから、 \begin{align*} \mathbb{log}_e{\alpha^{-1}} &= - \log_e{\abs{\alpha}} - i\cdot\theta - i\cdot 2k^\prime\pi + i\cdot 2k\pi \\ &= - \left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2(k^\prime - k)\pi\right) \end{align*} であり、$k^\prime - k$ は常に整数であるから（または整数全体の集合と言い換えてもいい）$l = k^\prime - k$ とすれば \begin{align*} \mathbb{log}_e{\alpha^{-1}} = - \left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2l\pi\right) = - \mathbb{log}_e{\alpha} \end{align*} となる。 上に述べた結果を合わせてまとめると \begin{align*} \mathbb{log}_e{\alpha^{-1}} = \mathbb{log}_e{\frac{1}{\alpha}} = - \mathbb{log}_e{\alpha} \;. \end{align*}

$\bullet\; \mathbb{log}_e{\alpha^{\frac{1}{j}}} = \dfrac{1}{j}\mathbb{log}_e{\alpha} \;\text{（$j$ は整数）}$

やはり同様に \begin{align*} \mathbb{log}_e{\alpha^\beta} = \beta \mathbb{log}_e{\alpha} + i\cdot 2k\pi \quad(k = 0, \pm 1, \pm 2, \ldots) \end{align*} において $\beta = 1/j$ つまり分子１の有理数の場合を考えてみる。 当然、この $j$ は整数である。また $k,\, k^\prime$ が整数であることも今までと同じ。 計算を進めると \begin{align*} \mathbb{log}_e{\alpha^{\frac{1}{j}}} &= \frac{1}{j}\mathbb{log}_e{\alpha} + i\cdot 2k\pi \\ &= \frac{1}{j}\left(\log_e{\abs{\alpha}} + i\cdot\arg(\alpha)\right) + i\cdot 2k\pi \\ &= \frac{1}{j}\left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2k^\prime\pi\right) + i\cdot 2k\pi \\ &= \frac{1}{j}\left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2k^\prime\pi + i\cdot 2kj\pi\right) \\ &= \frac{1}{j}\left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2(k^\prime + kj)\pi\right) \end{align*} であり、$k^\prime + kj$ は常に整数であるから $l = k^\prime + kj$ と置き換えて \begin{align*} \mathbb{log}_e{\alpha^{\frac{1}{j}}} = \frac{1}{j}\left(\log_e{\abs{\alpha}} + i\cdot\theta + i\cdot 2l\pi\right) = \frac{1}{j}\mathbb{log}_e{\alpha} \quad(j = 0, \pm 1, \pm 2, \ldots) \end{align*} を得る。

$\bullet\; \left(\alpha^\frac{1}{j}\right)^\beta = \alpha^\frac{\beta}{j} \;\text{（$j$ は整数）}$

上のこの結果を $\displaystyle{ \left(\alpha^\frac{1}{j}\right)^\beta }$ に適用すると次のように興味深いことがらがあらわれてくる： \begin{align} \left(\alpha^\frac{1}{j}\right)^\beta = e^{\beta \mathbb{log}_e{\alpha^\frac{1}{j}}} = e^{\frac{\beta}{j}\mathbb{log}_e{\alpha}} = \alpha^\frac{\beta}{j} \;. \label{eq.c.01} \end{align} つまり、$1/j$ はカッコの中から外に出ることができる。 一般にはこの逆、つまり $\left(\alpha^\beta\right)^\frac{1}{j}$ と等しくないことは、指数法則ののところですでにみた。

$\bullet\; \left(\alpha^\beta\right)^j = \alpha^{\beta j} = \alpha^{j \beta} \neq \left(\alpha^j\right)^\beta \;\text{（$j$ は整数）}$

指数のどちらかが整数である、という場合に絞った考察である（以下、$k$ は整数）。 $\left(\alpha^\beta\right)^j$ について定番の式変形をおこなうと \begin{align*} \left(\alpha^\beta\right)^j = e^{j \mathbb{log}_e{\alpha^\beta}} = e^{j (\beta\mathbb{log}_e{\alpha} + i\cdot 2k\pi)} = e^{j\beta\mathbb{log}_e{\alpha} + i\cdot 2kj\pi)} = e^{j\beta\mathbb{log}_e{\alpha}}e^{i\cdot 2kj\pi} = e^{j\beta\mathbb{log}_e{\alpha}} = \alpha^{j\beta} = \alpha^{\beta j} \end{align*} となる。$2kj$ が整数であるから不定性が出てこなくなる。 一方で $\left(\alpha^j\right)^\beta$ においては \begin{align*} \left(\alpha^j\right)^\beta = e^{\beta \mathbb{log}_e{\alpha^j}} = e^{\beta (j\mathbb{log}_e{\alpha} + i\cdot 2k\pi)} = e^{j\beta\mathbb{log}_e{\alpha} + i\cdot \beta \cdot 2k\pi} = e^{j\beta\mathbb{log}_e{\alpha}}e^{i\cdot \beta \cdot 2k\pi} \end{align*} となり不定性があらわに出てきてしまう。 したがって \begin{align*} \left(\alpha^\beta\right)^j = \alpha^{j\beta} \neq \left(\alpha^j\right)^\beta \end{align*} とまとめることができよう。 つまり、外側の指数が整数である場合にはカッコが外れるけれども、中側の指数のみが整数のときはカッコは解けないのである（両方が整数の場合には問題ないことは、指数法則のところで見た）。

$\bullet\; -1$ の特殊性

ただし $-1$ は例外。 今求めた結果において $j = -1$ とすると \begin{align*} \left(\alpha^\beta\right)^{-1} = \alpha^{-\beta} \iff \frac{1}{\alpha^\beta} = \alpha^{-\beta} \end{align*} という結果が得られるし、\eqref{eq.c.01} において $j = -1$ とすると \begin{align*} \left(\alpha^\frac{1}{-1}\right)^\beta = \alpha^\frac{\beta}{-1} = \alpha^{-\beta} \end{align*} であるから \begin{align*} \left(\alpha^\beta\right)^{-1} = \left(\alpha^{-1}\right)^\beta = \alpha^{-\beta} \end{align*} であり、かつ \begin{align*} \alpha^{-\beta} = \frac{1}{\alpha^\beta} = \left(\frac{1}{\alpha}\right)^\beta \end{align*} という結果も得られるのである。 これは、上での結論である「中側の指数のみが整数の時はカッコ解けない」ということに反しているのだが、どうとらえればいか？ とにかく、$-1$ は例外で、$-1$ はカッコの内外で「行ったり来たり」が可能なのである。

さらに付け加えれば、指数法則をもちいると \begin{align*} \left(\frac{1}{\alpha}\right)^\beta = \frac{1^\beta}{\alpha^\beta} = \frac{1}{\alpha^\beta} \end{align*} ということから $1^\beta$ はやはり $1$ になっている。 すなわち、$1$ の複素数乗もつねに$1$ なのである。

$\square$ まとめ

複素数の世界での指数法則をまとめておこう。

• 条件

  複素指数関数、偏角関数（$\arg$）、複素対数関数が定義されていること。 特徴的な事柄は次の通り。 \begin{align*} & \arg(zw) = \arg(z) + \arg(w) \\ & \arg(z/w) = \arg(z) - \arg(w) \\ \\ & \mathbb{log}_e{(zw)} = \mathbb{log}_e{z} + \mathbb{log}_e{w} \\ & \mathbb{log}_e{(z/w)} = \mathbb{log}_e{z} - \mathbb{log}_e{w} \end{align*}

• 定義

  \begin{align*} & \alpha^\beta \equiv e^{\beta \mathbb{log}_e{\alpha}} \\ & e^0 \equiv 1 \end{align*}

• 基本指数法則

  複素指数関数については常に \begin{align*} e^{z+w} = e^z e^w \;. \end{align*} 一般形については、同じ $\arg(\alpha)$ を用いる場合に限って \begin{align*} \alpha^{\beta + \gamma} = \alpha^\beta \alpha^\gamma \;. \end{align*}

• 指数法則

  \begin{align*} & (\alpha\beta)^\gamma = \alpha^\gamma \beta^\gamma \\ \end{align*} は常に成立する。 また、一般には $\left(\eta^\alpha\right)^\beta = \left(\eta^\beta\right)^\alpha = \eta^{\alpha\beta}$ は成立しない。

• 整数指数の特殊性

  $k,\, l$ はともに整数であるとする。 そのとき \begin{align*} \left(\alpha^k\right)^l = \left(\alpha^l\right)^k = \alpha^{kl} \end{align*} は成立する。 また \begin{align*} \left(\alpha^\beta\right)^k = \alpha^{k\beta} \quad \text{（$\alpha^{k\beta} \neq (\alpha^k)^\beta $ であることに注意）} \end{align*} も成立する（本稿初頭で述べた「生い立ち」の考えがきちんと踏襲されている）。 さらに \begin{align*} \left(\alpha^\frac{1}{k}\right)^\beta = \alpha^\frac{\beta}{k} \quad \text{（$\alpha^\frac{\beta}{k} \neq (\alpha^\beta)^\frac{1}{k}$ であることに注意）} \end{align*}

• $-1$ の特殊性

  \begin{align*} & \alpha^{-1} = \frac{1}{\alpha} \\ &\left(\alpha^\beta\right)^{-1} = \left(\alpha^{-1}\right)^\beta \end{align*}

• 付随的指数法則

  \begin{align*} & \left(\frac{1}{\alpha}\right)^\beta = \frac{1}{\alpha^\beta} \\ & \left(\frac{\alpha}{\beta}\right)^\gamma = \frac{\alpha^\gamma}{\beta^\gamma} \end{align*}

---

Appendixes

$\bigstar$ appendix1 : $AB = 0 \;\iff\; A = 0 \;or\; B = 0$

まず、$A,\, B$ 共に実数であるならば、$AB \neq 0 \iff \text{$A$ と $B$ はともに $0$ ではない}$、という事柄は自明としていいはずである。 では、複素数まで範囲を広げるとどうだろうか？

２つの複素数を、$a,\, b,\, c,\, d$ を実数、$i$ を純虚数（すなわち、$i^2 = -1$）として $z_1 = a + ib$、 $z_2 = c + id$ とあらわすと \begin{align*} z_1 z_2 = (a + ib)(c + id) = (ac - bd) + i(ad + bc) \end{align*} となる。したがって \begin{align*} z_1 z_2 = 0 \iff ac - bd = 0 \,(1) \;\text{かつ}\; ad + bc = 0 \,(2) \end{align*} ということになる。さてここで $(1) \times d - (2) \times c$ を計算すると \begin{align*} (ac - bd)d - (ad + bc)c = 0 \iff b(d^2 + c^2) = 0 \iff b = 0 \;\text{または}\; c = d = 0 \end{align*} であるから、$c = d = 0$ の時は $z_2 = 0$ である。 $b=0$ の時は $(1),\, (2)$ から $ac = 0 \;\text{かつ}\; ad = 0$ が成り立たねばならず、任意の $c,\, d$ でこれが成立するためには $a = 0$ でなくてはならない。 それ故、$b = a =0$ となって $z_1 = 0$ となる。 つまり、$z_1 z_2 = 0 \iff z_1 = 0 \;\text{または}\; z_2 = 0$。

一応、格好をつけた（？）別のやり方も。 $z_1 = r_1(\cos\theta_1 + i\sin\theta_1)$、 $z_2 = r_2(\cos\theta_2 + i\sin\theta_2)$ という、実数 $r_1,\, r_2,\, \theta_1,\, \theta_2$ を用いた極形式であらわすと \begin{align*} z_1 z_2 &= r_1(\cos\theta_1 + i\sin\theta_1) \cdot r_2(\cos\theta_2 + i\sin\theta_2) \\ &= r_1r_2\Bigl\{ \bigl( \cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2 \bigr) + i \bigl( \sin\theta_1\cos\theta_2 + \cos\theta_1\sin\theta_2 \bigr) \Bigr\} \\ &= r_1r_2\Bigl\{ \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \Bigr\} \end{align*} となる（三角関数の加法定理を利用）。 三角関数の性質から $\cos(\theta_1 + \theta_2)$ と $\sin(\theta_1 + \theta_2)$ がともに同時に $0$ になることはあり得ないので、$z_1 z_2$ が $0$ となるときは、$r_1$ が $0$（すなわち $z_1 = 0$）かまたは $r_2$ が $0$（つまり $z_2 = 0$）のときに限られる。

これらの結果を命題論理を用いてあらわすと \begin{align*} z_1 z_2 = 0 \iff z_1 = 0 \;\text{または}\; z_2 = 0 \end{align*} であり、対偶を取れば \begin{align*} z_1 z_2 \neq 0 \iff z_1 \neq 0 \;\text{かつ}\; z_2 \neq 0 \end{align*} となる。 したがって、複素数まで範囲を広げても、$AB \neq 0$ という条件は、$A,\, B$ ともに $0$ ではないという条件でまかなえるのであった。

---

$\bigstar$ appendix2 : $n$ 乗根を求める計算の詳細

「指数が有理数のとき」に $n$ 乗根にまつわる生態を見たが、そのときに用いた $n$ 乗根の計算をここに記しておく。

• $\set{1^\frac{1}{2}} = \set{1,\; -1}$

  $x^2 = 1$ を解けば良いので \begin{align*} & x^2 = 1 \iff x^2 - 1 = 0 \iff (x + 1)(x -1) = 0 \\ & \therefore x = 1,\; -1 \;. \end{align*}

• $\set{(-1)^\frac{1}{2}} = \set{i,\; -i}$

  まず \begin{align*} & x^2 = (-1) \iff x^2 + 1 = 0 \iff (x + i)(x - i) = 0 \\ & \therefore x = i,\; -i \;. \end{align*} である。 ついでに $a \gt 0$ とすれば \begin{align*} & x^2 = (-a) \iff x^2 + a = 0 \iff (x + \sqrt{a}i)(x - \sqrt{a}i) = 0 \\ & \therefore x = \sqrt{a}i,\; -\sqrt{a}i \end{align*} となるので $\set{a^\frac{1}{2}} = \set{\sqrt{a}i,\; -\sqrt{a}i}\;(a > 0)$ である。

• $\set{1^\frac{1}{3}} = \set{1,\; \dfrac{-1 + \sqrt{3}i}{2},\; \dfrac{-1 - \sqrt{3}i}{2}}$

  \begin{align*} x^3 = 1 \iff x^3 - 1 = 0 \iff x^3 - 1^3 = 0 \iff (x - 1)(x^2 + x + 1) = 0 \end{align*} であるから、$x = 1$ は解。もうひとつのカッコについては \begin{align*} x^2 + x + 1 = 0 \iff x = \frac{-1 \pm \sqrt{1^2 - 4 \times 1}}{2} = \frac{-1 \pm \sqrt{3}i}{2} \end{align*} である。

• $\set{(-1)^\frac{1}{3}} = \set{-1,\; \dfrac{1 + \sqrt{3}i}{2},\; \dfrac{1 - \sqrt{3}i}{2}}$

  \begin{align*} x^3 = -1 \iff x^3 + 1 = 0 \iff x^3 + 1^3 = 0 \iff (x + 1)(x^2 - x + 1) = 0 \end{align*} であり \begin{align*} x^2 - x + 1 = 0 \iff x = \frac{1 \pm \sqrt{(-1)^2 - 4 \times 1}}{2} = \frac{1 \pm \sqrt{3}i}{2} \end{align*} である。

• $\set{i^\frac{1}{3}} = \set{-i,\; \dfrac{i + \sqrt{3}}{2},\; \dfrac{i - \sqrt{3}}{2}}$

  $i^3 = i \times i \times i = -i$ を利用する。 \begin{align*} x^3 = i \iff x^3 - i = 0 \iff x^3 + i^3 = 0 \iff (x + i)(x^2 -ix + i^2) = (x + i)(x^2 -ix - 1) = 0 \end{align*} であり \begin{align*} x^2 - ix - 1 = 0 \iff x = \frac{i \pm \sqrt{(-i)^2 - 4 \times (-1)}}{2} = \frac{i \pm \sqrt{3}}{2} \end{align*} である。

• $\set{(-i)^\frac{1}{3}} = \set{i,\; \dfrac{-i + \sqrt{3}}{2},\; \dfrac{-i - \sqrt{3}}{2}}$

  \begin{align*} x^3 = -i \iff x^3 + i = 0 \iff x^3 - i^3 = 0 \iff (x - i)(x^2 +ix + i^2) = (x - i)(x^2 +ix - 1) = 0 \end{align*} であって \begin{align*} x^2 + ix - 1 = 0 \iff x = \frac{-i \pm \sqrt{i^2 - 4 \times (-1)}}{2} = \frac{-i \pm \sqrt{3}}{2} \end{align*} である。

利用はしなかったが、おまけとして $\set{i^\frac{1}{2}},\; \set{(-i)^\frac{1}{2}}$ も計算しておこう。 $x^2 = i$ の解が $a + bi$（$a,\, b$ は実数）であるとすると \begin{align*} (a + bi)^2 = i \iff a^2 + 2abi - b^2 = i \end{align*} であるから、複素数の相等の定義より $2ab = 1,\; a^2 - b^2 = 0$ でなければならないことになる。 ここで $a^2 - b^2 = 0 \iff (a+b)(a-b) = 0$ であるから、$a = b$ または $a = -b$ と言える。 しかしながら $a = -b$ の場合では、$2ab = 1 \iff b^2 = -1/2$ となって、このような実数 $b$ は存在しない。 それゆえ、$a = b$ でなければならず、かつ、$2ab = 1$ であるから \begin{align*} 2ab = 1 \iff a^2 = \frac{1}{2} \iff a = \sqrt{\frac{1}{2}} \quad\text{or}\quad -\sqrt{\frac{1}{2}} \end{align*} ともとまり、結果として $i$ の平方根は \begin{align*} \set{i^\frac{1}{2}} = \set{\sqrt{\frac{1}{2}} + \sqrt{\frac{1}{2}} i,\quad -\sqrt{\frac{1}{2}} - \sqrt{\frac{1}{2}} i} \end{align*} となる。

$x^2 = -i$ のときもほぼ同様で \begin{align*} & (a + bi)^2 = -i \iff a^2 + 2abi - b^2 = -i \\ & \therefore 2ab = -1 \quad\text{and}\quad \{a = b \quad\text{or}\quad a = -b \} \end{align*} $a=b$ の場合では $2ab = -1 \iff b^2 = -1/2$ となって $b$ は存在しない。 それゆえ $a = -b$。 したがって、$a = \pm \sqrt{1/2}$。 すなわち \begin{align*} \set{(-i)^\frac{1}{2}} = \set{\sqrt{\frac{1}{2}} - \sqrt{\frac{1}{2}} i,\quad -\sqrt{\frac{1}{2}} + \sqrt{\frac{1}{2}} i} \;. \end{align*}

---

$\bigstar$ appendix3 : 実数の $n$ 乗根と $n$ の偶奇性

$x,\, y$ を実数として、$y = x^n$ という $n$ 次方程式を考える。 もちろん $n$ は自然数。 見方を逆にすれば、$x$ は $y$ の $n$ 乗根ということになる。 さてこの $n$ 乗根のうちで実数であるものはいくつあるのだろうか？

$n$ 次方程式を、$n$ の偶奇（even、odd）によって場合分けする、という方法を取ろう。 $m$ も自然数とすれば、$y = x^n$ は \begin{alignat*}{2} & y = x^{2m} & &\quad (n = 2m: even) \\ & y = x^{2m - 1} & &\quad (n = 2m-1: odd) \end{alignat*} と分類できる。 ここで初等的な解析学の力を借りる。 各々の導関数は \begin{align*} & y^\prime = 2m x^{2m - 1} \\ & y^\prime = (2m - 1) x^{2(m - 1)} \end{align*} と求まるから、関数の増減表を書いてみると \begin{align*} \text{n: even} \quad \begin{array}{r|c|c|c} \hline x & \cdots & 0 & \cdots \\ \hline y^\prime & - & 0 & + \\ \hline y & \searrow & 0 & \nearrow \\ \hline \end{array} \;, \qquad \text{n: odd} \quad \begin{array}{r|c|c|c} \hline x & \cdots & 0 & \cdots \\ \hline y^\prime & + & 0 & + \\ \hline y & \nearrow & 0 & \nearrow \\ \hline \end{array} \quad \end{align*} とまとめられる。 $n$ が偶数（even）の時は、$x = 0$ を境にして単調減少から単調増加、$n$ が奇数（odd）のときは常に単調増加である関数になっている。 試しに $y = x^3$ と $y = x^4$ のグラフを書いてみると次の通りで、関数の振る舞いが実感できる。

原点付近を拡大すると $x = 1$ の付近を見てみると 以上の事実から $y = x^n$ においては、 \begin{align*} & n: odd \Rightarrow y \;\text{の実数の $n$ 乗根は一つのみ存在する} \\ & n: even \Rightarrow \begin{cases} y \gt 0 \;\text{の時には実数の $n$ 乗根は $2$ 個} \\ y = 0 \;\text{の時には実数の $n$ 乗根は $0$ 一つしかない} \\ y \lt 0 \;\text{の時には実数の $n$ 乗根は存在しない} \end{cases} \end{align*} ということが導かれる。

---

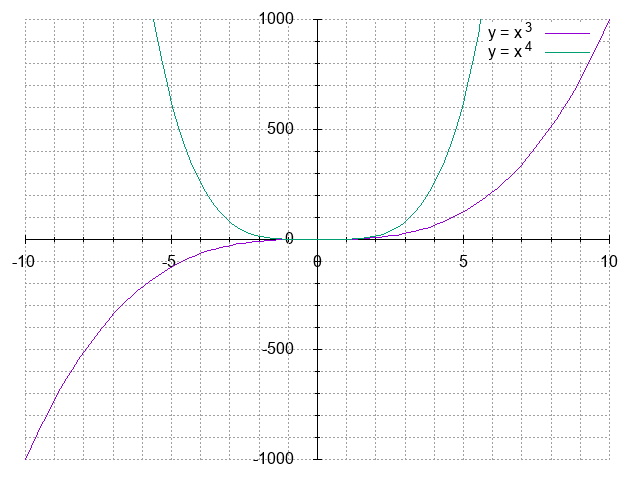
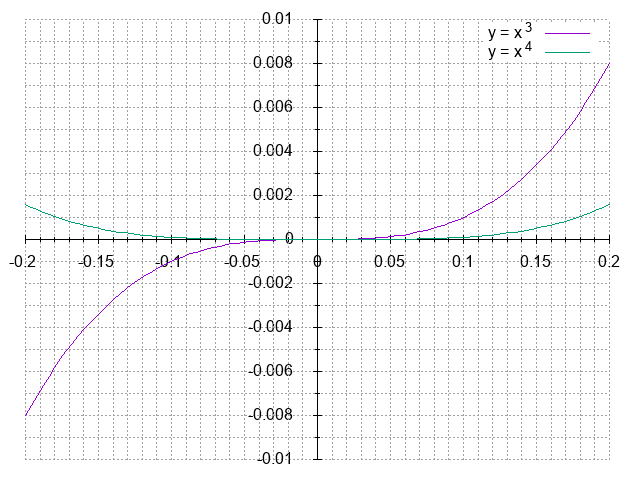
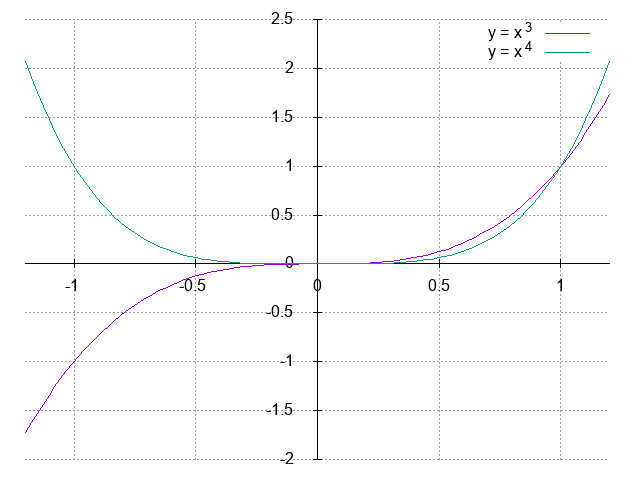
$\bigstar$ appendix4

appendix3 の考察を $1 = x^n$ に応用すると、 \begin{align*} & n: odd \Rightarrow 1 \;\text{の実数の $n$ 乗根は $1$ のみ} \\ & n: even \Rightarrow 1 \;\text{の実数の $n$ 乗根は $1$ と $-1$} \end{align*} ということになる。ここで $a,\, b$ を任意の実数（但し $b \neq 0$）とし、$\left(\dfrac{a}{b}\right)^n = 1$ を考えると、

• $n: odd$ のとき

  $\displaystyle{ \left(\frac{a}{b}\right)^n = 1 \iff \frac{a}{b} = 1 \iff a = b }$

• $n: even$ のとき

  一般には、 $\displaystyle{ \left(\frac{a}{b}\right)^n = 1 \iff \frac{a}{b} = \pm 1 \iff a = \pm b }$ であり、$a,\, b$ ともに正の数であるならば $a = b$ しかあり得ない。

という結果になる。

---

エピローグ

いろいろと寄り道をしていて、書き上げるまでにかなり時間がかかってしまった。 とくに指数が有理数のときの生態について、悩ましいところも多く、結局複素数の根まで考えることになってしまった。

複素数の世界については、Internet 上の 新潟大学工学部のこのページのコンテンツ（URL は http://www.eng.niigata-u.ac.jp/~nomoto/2.html） に大変お世話になった。 新しい発見がたくさんあり、とても良い勉強になった。 著者のお名前にたどり着けなかったのでこのような紹介になってしまっている。 失礼があればお許しいただきたい。 あわせて、山本直樹著『複素関数論の基礎』（裳華房、第4版第1刷（2019））もよく紐解いた。 とりわけ複素数というものを曖昧にとらえていたわたくしが、複素数と複素関数の基礎について再度考える際に、とてもためになる本であった。

ともあれ、右往左往した結果、例によって冗長な雑文になってしまっている。 ま、それも、自分の鉛筆で計算したという証であると、自らを慰めたい。 切れ味の良い頭脳をお持ちの方には、あきられるに違いあるまい。 善戦苦闘であったら、と願っております。

---